![]()
![]()
| 1,極座標 | 座標 座標変換 速度 加速度 |
| 2,運動の法則 | テイラー展開 運動の法則 |
| 3,実際の運動 | 微少 惑星の運動 |
| 4,仕事 | 保存力 ポテンシャル 運動量 |
![]()
今まで高校では、物体の位置を表すときに(x,y,z)座標を使ってきました。
しかし、ほかにも表し方があります。例えば、自分の家を伝えるときには、
「南大沢駅の北西に500m」や「○○駅の西に350m北に350m」
「北緯35°40′東経140°13′」という表現があります。
物理の世界でも同じです。
物理では、以下の3つの座標を用います。
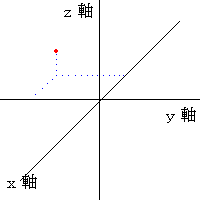
これは、いままでよく用いてきた(x,y,z)座標です。
これを、「デカルト座標」といいます。
座標の取り方は図の通りで、手前がx、右がy、上がzになります。
つまり、左手の「中指」「人差し指」「親指」の順番です。
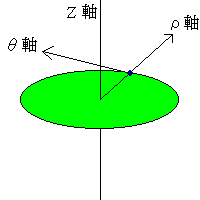
これはデカルト座標のz軸はそのままで、xをyをρとθで表します。
ρはz軸からの距離、θはy軸とρ軸となす角を意味します。
この座標は、物体の位置が変化するとρ軸とθ軸の向きが変化します。
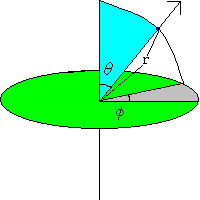
物理でよく用いられるのがこの座標です。(r,φ,θ)を用います。
rは基準点からの距離、φはy軸となす角、θはz軸となす角です。
![]()

デカルト座標(x,y,z)と円柱座標(ρ,θ,z)の変換は
ρ=(x2+y2)1/2 θ=atn(y/x) z=z
第1式は、ρがx,yで構成される距離で表せることを意味します。
第2式は、tanθ=y/xで表せるので、arctanでθが求まります。
第3式は、zの座標変換はないので変わらないことを意味します。
その反対の変換は、
x=ρ cosθ y=ρ sinθ z=z
と簡単に表せます。

デカルト座標(x,y,z)と極座標(ρ,θ,φ)の変換は
x=r sinθ cosφ y=r sinθ sinφ z=r cosθ
この変換は非常に重要なのでよく覚えてください。
(以前、yについての変換式で、sin φのところがcosφになっていました。)
![]()
ここでは、極座標の速度がどのようになるかを考えます。
極座標は、物体の位置が変化するとともに軸の向きが変わってしまいます。
そのため、速度は次のように表せます。
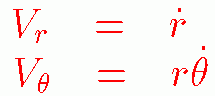
ここで、θ' は、θの時間微分、dθ/dtを表します。
vθはθ'の前にrがかけられているので注意してください。
デカルト座標では、xの速度はx' yの速度はy' と簡単になるのですが
極座標では、少し複雑になります。

![]()
ここでは、極座標の加速度がどのようになるかを考えます。
加速度も速度のように
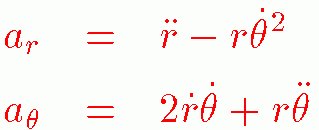
ここで、θ'' は、θの時間2階微分、d2θ/dt2を表します。
デカルト座標では、xの加速度はx'' yの加速度はy'' と簡単になるのですが
極座標では、複雑になります。
![]()
![]()
世の中にある微分可能な関数はすべてテイラー展開をすることによって次のようにできます。
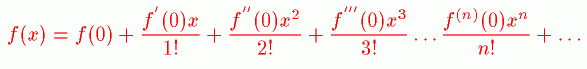
これと似たものにマクロニー展開というものがあります。これは関数を
x=xoで近似したのではなく、x=0
で展開したときの近似式なのです。(今回のように)

これを書き直すと次のような重要公式ができます。
eix = cosx + i sinx
![]()
第1法則は、慣性の法則といいます。
これは、物体に外部から力を与えない限り、物体は直線上の運動の状態を
そのまま続けるというものです。
F=ma
この式を「運動方程式」と呼んできました。
物理理の世界では、次のようにも書きます。
F=mr''
これは、加速度を位置座標rの時間2階微分であるといっています。
これは、「作用・反作用の法則」ともいわれています。
物体AがBに力Fを及ぼしているとすると、
BはAに力−Fを及ぼしているというものです。
![]()
![]()
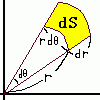
円や球体についての物理的な計算をするとき、微少面積(体積)に
分割し、それに物理的な計算をして、再び積分して全体の
物理量を求めることがある。
円の場合、微少面積は長方形に近似します。(上図参照)
r方向の長さをdr,θ方向の長さはrdθになります。
面積はrdrdθになります。
これをθ方向に0から2πまで積分し、さらにr方向に積分すれば
面積が求まります。微少面積での物理量はrdrdθの段階で計算します。
球体の場合は、今のものに高さrsinθdψが加わって、
微少体積がr2sinθdrdθdψになります。

![]()
太陽系で、太陽の周りを回っている惑星の軌道について考えます。
惑星に働く力は中心力(r軸方向の力)のみです。
運動方程式は次の通りです。
Fr=m(r''−rθ'2) Fθ=m(2r'θ'+rθ'')
先ほどの第1式を変形すると次のようになります。
m(r''−rθ'2)=−GMm r2
r= λ 1+εcos(θ+α)
λ= l l:角運動量 GMm2 G:万有引力定数 M:太陽の質量 ε= Cl2 m:惑星の質量 GMm C,α:定数(積分定数)
このεによって、運動が変わります。
|ε|<1 楕円軌道 |ε|=1 円軌道 |ε|>1 双曲線軌道
先ほどの第2式を変形すると次のようになります。
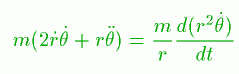
このことからr2θ'が時間に対して一定であることがわかります。
これが、ケプラーの第2法則の「面積弧一定の法則」です。
![]()
![]()
保存力は、力が場所によってのみ決まっているものを意味します。
だから、摩擦があったりすると保存力とはいえません。
保存力の例としては、重力、磁力、電気力などがあります。
(いずれもFがrの2乗に逆比例する)
さらに保存力を積分するとエネルギーになります。つまり
U=−∫F・dr
という関係があります。負号に気をつけてください。これから、
F=−∂U U:位置エネルギー ∂r
という式ができます。これは、重力,電荷などで利用します。
ポテンシャルとは位置エネルギーのことです。
先ほど、「保存力」をやりましたが、そのときの位置エネルギーUが
ポテンシャルといわれます。
![]()
T=1mx'2 T:運動エネルギー 2
これをx′で微分すると
∂T =mx'=p p:運動量 ∂x' x':速度
これはよく使う公式です。運動量は実はこのように定義されています。
![]()
ひとこと力学は、いろいろな知識が必要で、これ以外にも剛体波動や解析概説の |