![]()
![]()
| 1,剛体 | 角運動量L 慣性モーメントI L,I,N に関する諸公式 回転体の運動方程式 物体の変形 E,σ,k,n |
| 2,流体 | ベルヌーイの原理 層流・乱流 ニュートン流体 |
| 3,波動 | 振動 波動方程式 フェルマーの原理 |
![]()
剛体を考える上で次の式を知る必要があります
N = r × F L = r × p I = mr2
| N:力のモーメント F:ベクトル r:位置ベクトル |
L:角運動量 p:運動量 I:慣性モーメント m:物体の質量 |
力のモーメントは、何かものを回すときの強さのようなものです。
例えば、ねじ回しの場合、中心からの距離が遠い(rが大きい)ほど
力(F)が小さくなります。
角運動量は、何かものが回転させるときのエネルギーのようなものです。
あなたが回転椅子に座っているならば、手を広でた状態で回転してみましょう。
このとき角運動量は保存されるので、手を縮める(rを小さくする)と、
回転が速くなる(pが大きくなるのでvが大きくなる)でしょう!
角運動量は、回転方向に力を受けない(中心力のみ)とき保存されます
回転モーメントは、何かものを回転させるときの、回転のしやすさということになります。
先ほどの椅子の例では、手を広げた状態では回転しにくい(Iが大きい)し、
縮めた状態では回転しやすい(Iが小さい)というわけです。
![]()
NとLの間には次の関係があります。
dL=N dt
これは、角運動量は力のモーメントを時間で積分したもので、
回転のエネルギーに似ています。(実際は違うが・・・)
次にIとLの間には次の関係があります。
L=r×p=Iω=Iθ′
これは、角運動量は慣性モーメントと回転速度の積であることを意味します。
次にIとNの間には次の関係があります。
Iθ″=F×r=N
これは、回転体の運動方程式です。詳しくは後ほどに解説します。
つぎに回転体の持つエネルギーの公式を解説します。
K=1Iω2 2
まるで運動エネルギーの公式にそっくりです。
平面板の公式があります。平面板の重心での回転モーメントをIgとします、
そこからhだけ離れたところでの慣性モーメントをあらわす式が
I=Ig+Mh2
です。 また、回転が組合わさっている場合場合
L=Lg+L′
Lgは回転体の重心の角運動量で、L′は重心から見た角運動量になる。
問題
円盤を面に垂直な軸で回転させたときの回転モーメントをIzとする。
円盤の直径を軸として回転させたときの慣性モーメントを求めよ
解答
Iz=Ix+Iy かつ、対象性からIx=Iyなので
Ix=Iy=1/2 Iz
回転モーメントを求めるときは円盤の場合、面積分をする必要がある
![]()
Iθ″=N
これが回転体の運動方程式です。
Iがまるで質量のようで、θがx、NがFに非常に似ています。
mx″=Fや先ほどの回転エネルギーの式に非常に似てます。
今の式を少し変形させて
Iθ″=F×r
は割と使うことがあります。
![]()
ここでは、弾性体に関係する公式をまとめておきます。
F=E⊿l E:ヤング率 S:面積 l:長さ S l
左辺のいわゆる圧力に相当します。右辺の⊿l/lは単位長さでどれだけ縮んだかを
意味します。Eがヤング率で物体によって決まっています。
σ=-⊿l’/l’ l :横(縦)の長さ ⊿l /l l’:縦(横)の長さ
これは、縦(横)一方を縮めると、横(縦)がどれだけのびるか
ということをあらわしたものです。
σはポアッソン比で物体によって決まっています。
⊿l/lについては前述のとおりです。
⊿p=-k⊿V p:圧力 k:体積弾性率 V:体積 V
これは、単位体積が⊿Vだけ変化すると、
圧力が-k⊿Vだけ変化しているのがわかる。
マイナスがあるのに注意してください。(∴体積は縮むので)
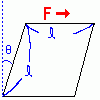
F =nθ n:剛性率 θ:ずれた角度 F:力 l2 l:立体の高さ,長さ
これは、右図のような直方体に力Fを加えたとき
どれだけ曲がるかという式です。(右図参照)
物体がθだけ変形しているとき、物体に蓄えられているエネルギーを
求める式があります。
U=1nθ2V=∫Ndθ n:剛性率 θ:ずれた角度 2 V:立体の体積 N:力のモーメント
エネルギーは、nとθを使っても表せ、力のモーメントでも表せます。
![]()
![]()
1ρv2 + ρgz + P=一定 ρ:密度 v:流体の速度 2 g:重力加速度 P:圧力
これは、エネルギー保存の式と考え方は同じです。
左辺第1項は、エネルギー保存の式での運動エネルギーに相当し、
第2項は、位置エネルギーです。第3項は圧力です。
これ全体が、圧力に関する式と考えてください。
![]()
R=ρaU ρ:流体の密度 a:管の半径 η U:平均流速 η:粘性(物体により一定)
管の中に流体を流すときの係数が上の式でR<1000で層流(流れがスムーズ)
で、R>1000で乱流(非常にながれにくい)になります。
乱流だとベルヌーイの法則か使えませんし、見かけの粘性が増したように見えます。
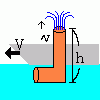
問題 速度Vで走っている船の底からくみ上げた水を 船の上から吹き出すときの速度をもとめよ 解答 ベルヌーイの法則より 1ρV2 + 0 + p =1ρv2 + ρgh + p 2 2 但し、圧力はどちらも同じでpとします。 vについて解くと v=(V2-2gh)1/2
![]()
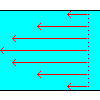
ニュートン流体は、流体を考える上で用いる仮想の流体です。
速度の違う流体がこすれるとき、お互いに及ぼす力は、こすれる面に垂直な方向の
速度勾配に比例するというのがニュートン流体です。
![]()
![]()
振動ではkという変数を用います。kは波数といって2πの長さにいくつの波
があるかを表したもので、式は
k=2π k:波数 λ:波長 λ
と、なります。
他に、波動方程式というものがあり、高度な波の状態を考える上で よく使います。
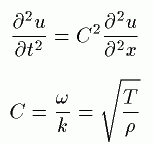 |
u:変位 C:波の速さ k:波数 ω:角速度 ρ:密度 T:張力 |
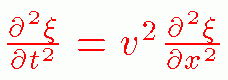
ξ:変位 v:波の速度
この特別解は、
平面波 ξ=Aexp{i(k・r±ωt)} 球面波 ξ=A exp{i(k・r±ωt)} r
この式から、次のようなシミュレーションができます。
波の干渉のアニメーション(21KB)
![]()
「光がA地点からB地点までいくときに、もっとも短時間で到達できる道を通る」
というのがフェルマーの定理です。
![]()
![]() Topに戻る
Topに戻る