![]()
![]()
| �P�C��ʉ����W | ��ʉ����W�E�^���� |
| �Q�C���O�����W���̕����� | ���O�����W�F�̕������@�I�C���[�̕������@�R���I���̗� |
| �R�C���������� | �n�~���g���̐����������@�|�A�\���̊��ʎ��@�ʑ���� |
![]()
���܂ŁA���W�Ɂi���C���C���j��p������i���C�ƁC�Ӂj��p�����̂�
���W�n�ɂ���ĈႢ������܂����B
���������ʂɕ\�����Ƃ����̂���ʉ����W�ł��B
���̍��W�́i���P�C���Q�C���R�C�E�E�E�j�ɂȂ�܂��B
���ꂩ��A���܂Ŏg���Ă����u�́v�C�u�^���ʁv�C�u���W�v��
��ʉ����W�ŕ\�����Ƃ��邽�߂̕ϊ��������Љ�܂��B
�i���P�C���Q�C�E�E�E�j�̍��W����ʉ����W�ŕ\���ƁA
��1=��1(��1,��2,��3,���)
��2=��2(��1,��2,��3,���)
�
�
��n=��n(��1,��2,��3,���)
�Ƃ����W������܂��B���ہA��1,��2,����ɂ͂��C���C���ₒ�C�ƁC�ӂ�����܂��B
�ł́A���ԂŔ�������ꍇ��
����i�����@�݂�i ��qJ �����@ J�@ ��qJ ����
�ɂȂ�܂��B���ꂩ��
�݂�i�����݂�i �݂�j���@�݂�j
�Ƃ��������ł��܂��B
��ʉ����ꂽ�͂́u�p�v�Ə����܂��B�u���v�Ƌ�ʂ��Ă��������B
�p�͎��̂悤�ɂ��ċ��߂܂��B
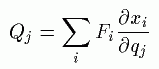
�܂��́A
�pj���|�݂t�@�@�@�@�t�F�ʒu�G�l���M�[ �@�@�@ �݂�j
���ꂩ��d���́A
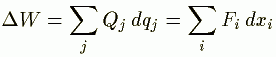
���̂悤�ɍ��܂ł̎d���̌v�Z�̂悤�ɂ��Ƃ܂�܂��B
��ʉ����ꂽ�^���ʂ͎��̕��@�ł��Ƃ߂��܂��B
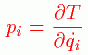
�s�F�^���G�l���M�[ ���F��ʉ����ꂽ�^����
�������ɂ���ƁA���Ȃ��݂̎��ɂȂ�܂��B
![]()
![]()
�����ɂk�����̂悤�ɒ�`���܂��B
�k���s�|�t�@�@�@�s�F�^���G�l���M�[�@�t�F�ʒu�G�l���M�[
���̂k�����O���W�A���Ƃ����܂��B
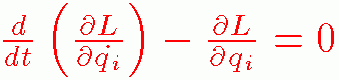
��������O�����W�F�̉^���������Ƃ����܂��B
����́A���܂ł̂e�������ɕς�鎮�ł��B
���̎��̈Ӗ�������̂́A���͍̂ŏ��̃G�l���M�[�ōςނ悤�ȉ^��������Ƃ������̂ł��B
���܂ł̉^�������������y�ɉ^�����������Ƃ��ł��܂��B
�i���C���C���j���W�ł́A���P�����@���Q�����@���R������������
���C���C���ɂ��ĉ^��������������A�������邱�Ƃɂ���ĉ^���������܂��B
���
���ݼ�ٴ�ٷް���t�i���j�ŕ\����镽�ʂ��^�����镨�̂̉^�������������߂�
��
�s���P���i��'2 �{ (����')2�j
�@�@�Q
�t���t�i���j
�k���P���i����2 �{ �i���Ɓ��j2�j�|�t�i���j
�@�@�Q
���ɂ��Ď������Ă��
���@�^�݂k�@�_�@�|�@�݂k���O
�����_�݂����^�@�@�@�݂�
��(������)�@�|�@������'2�@�|�@�݂t���O
�����@�@�@�@�@�@�@�@�@�@�@�@�@�݂�
��������������'2�{�݂t
�@�@�@�@�@�@�@�@�@�݂��E�E�E�E�E�E�E�E�E�E�@
���ɃƂɂ��Ď������Ă��
���@�^�݂k�@�_�@�|�@�݂k���O
�����_�݃Ɓ��^�@�@�@�݃�
���i����2 �Ɓ��j���O
����
����2 �Ɓ������E�E�E�E�E�E�E�E�E�E�E�E�E�A
�A�̍��ӂ͊p�^���ʂɑ�������B
�E�ӂ����ɂȂ��Ă��邱�Ƃ���A �p�^���ʂ��ۑ�����邱�Ƃ��킩��܂��B
�@�̍��ӂ͂��������̂����ɑ�������B
������E�ӂ͗͂ɑ������܂��B
�E�ӑ�P���͉��S�͂ɑ������A��Q���̓|�e���V�����ɂȂ��Ă��܂��B
�ȏ�̂悤�ɁA���O�����W�F�̕��������g���Ƌ@�B�I�ɉ^�����������Ƃ�
�ł��A�e�������ōl�����肸���Ɗy�ɂȂ�܂��B
�����A��ʉ��͂p�����l���Ă�������ɓ����Ă���ꍇ
���O�����W�F�̕����������̂悤�ɂ��čl���܂��B
�� �^�� �k�@�_�@�|�@�݂k�@���p �����_�݂�i���^�@�@�@�݂�i
�܂�A�E�ӂɈ�ʉ��͂p�������Ă�������̂ł��B
![]()
�I�C���[�̕������̓��O�����W�F�̕������ɂ�������ł��B
�� �^�݂e�@�_�@�|�@�݂e�@���O�@�@�@�@�e�F�͊w�ϐ� �����_�݂����^�@�@�@�݂� �����������^����
�I�C���[�̕������͕��̂��ŏ��i�G�l���M�[�C���ԂȂǁj��
�^�����邽�߂̓������Ƃ߂邱�Ƃ��ł��܂��B
���������āA���O�����W�F�̕������ɂ��������^����
�ŏ��̃G�l���M�[�ʼn^�����Ă���Ƃ����܂��B
���
�`�n�_����a�n�_�ɍs���Ƃ��ɍł��߂����̂�́H
��
���̂�h���炄��
�@�@�@�@����(�P�{����2)1/2����
�e��(�P�{����2)1/2�Ƃ��ăI�C���[�̕������ɑ�������
���@�^�@�@�@�����@�@�_�@���@�O
�����_(�P�{����2)1/2�^
�����ό`�����
���������@�ƂȂ�܂��B
�܂�A��������ԋߓ��Ƃ������Ƃł��B
![]()
���܁A���~���Ă�����W�n�i���C���C���j����
��]���Ă�����W�n�i�w�C�x�C�y�j�ɕϊ�����ꍇ���l���܂��B
�����w cos��t�|�xsin��t
�����w sin��t�{�xcos��t
������
�s���P���i��'2�{��'2�{��'2�j
�@�@�Q
�t���t�i���C���C���j
���́i���C���C���j�n�̎��Ɂi�w�C�x�C�y�j�n�̎��������A
�k���s�|�t�@�łk�����肵�A�w�C�x�C�y�ɂ���
���O�����W�F�̕����������Ă��
���w�����|�݂t�{�Q���ւx'�{����2�w�E�E�E�E�E�@
�@�@�@�@�@�݂w
���x�����|�݂t�|�Q���ւw'�{����2�x�E�E�E�E�E�A
�@�@�@�@�@�݂x
���y�����|�݂t
�@�@�@�@�@�݂y
�@,�A���̑�R���͉��S�͂ɂ��͂ŁA
��Q���̓R���I���̗͂Ƃ����܂��B
�ȏ�̖�肩��R���I���̗͂�
�Q���i�����~�ցj
�ŁA��`����܂��B���ꂩ��A�R���I���̗͂͑��x�ɔ�Ⴕ
��]���x�ɔ�Ⴕ�܂��B��C���̉�]�̌����́A
����ɂ��܂��B
![]()
![]()
�����ŁA�g�����̂悤�ɒ�`���܂��B
�g���s�{�t�@�@�@�s�F�^���G�l���M�[�@�t�F�ʒu�G�l���M�[
���̂g���n�~���g�j�A���Ƃ����܂��B�����قǂ̂k�Ǝ��Ă���̂Œ��ӂ��Ă��������B
�g�����Ƃ߂�Ƃ��A��̂悤�Ȏ����g���̂ł������ۂɂs�Ƃt���킩��Ȃ����Ƃ�����܂��B
�����ɂ́A���̕��@�ł��Ƃ߂܂��B
�g(q,p,t)������i��i���|�k(q,q��,t)�@�@�k�F���O���W�A�� �@�@�@�@�@ i�@�@�@�@�@�@�@�@�@�@�@�@ ���F�^����
�����ŁA���O���W�A�����i���C�����C���j�ł���킵
�n�~���g�j�A�����i���C���C���j�ŕ\�����Ƃɒ��ӂ��Ă��������B
�n�~���g�j�A���ɂ͎��̊W������܂��B
����i���݂g �@�@�@�@�g�F�n�~���g�j�A�� ���� �@�݂�i�@�@�@�@���F�^���� ����i���|�݂g ���� �@�@�݂�i
�Q�Ԗڂ̎��̉E�ӂɃ}�C�i�X������̂ɒ��ӂ��Ă�������
������n�~���g���̐����������Ƃ����܂��B
![]()
[u,v]
q p�@�@�����^�݂��@�݂��@�| �݂��@�݂� �_ i �_�݂�i �݂�i �@ �݂�i �݂�i�^
�Ƃ������Ƃ��`���Ă��܂��B
���܁A�e�i���C���C���j�Ƃ����͊w�ϐ����`���܂��B
��������Ԃ��őS��������ꍇ���l���܂��B
���e���݂e�{���^�݂e ��i���{�݂e ��i���_
�����@�݂��@���_�݂�i �@�@�@�݂�i�@�@�@�^
���݂e�{���^�݂e �݂g �|�݂e �݂g �_
�@�݂��@���_�݂�i �݂�i �@�݂�i �݂�i�^�@�@�搳��������
���݂e�{�m�e�C�g�nq p
�@�݂�
�͊w�ϐ��e�ɂ��Ƃ����ϐ����܂܂�Ă��Ȃ���
���e���m�e�C�g�nq p ����
�ɂȂ�܂��B
![]()
�ʑ���Ԃ́A���������C���������ɂ������̂��ʑ���Ԃł��B
�ꎟ���a�U���q�┠�̒����^�����镨�͓̂����I�Ȍ`�ɂȂ�܂��B
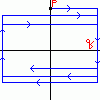 ���̒��̕��̂��ǂɏՓ˂��Ȃ��猸�����Ă����^��
���̒��̕��̂��ǂɏՓ˂��Ȃ��猸�����Ă����^��
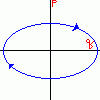 �P�����a�U���q�̉^��
�P�����a�U���q�̉^��
![]()