![]()
![]()
| 1,sch.eg.の解法 | 期待値 ハイゼンベルグ描像 球面調和関数 ベッセル関数 |
| 2,反転 | パリティ 汎関数 |
| 3,角運動量 | 角運動量演算子 スピン 角運動量の合成 同種粒子 |
| 4,摂動論 | 縮退のない場合 縮退のある場合 時間に依存する場合 変分法 半古典近似 |
今まで、波動関数はψ(r,t)で表しました。
しかし関数は成分が無限個あるベクトルであるとも考えら得ます。
そこで次のように書きます。
ψ(r,t) → |ψ>
この、|ψ>というのは縦ベクトルです。反対に<ψ|というのは横ベクトルです。
従って次のようなことがいえます。
/ψ1\ |ψ>=| : | \ψn/ <ψ|=(ψ1・・・ψn) <ψ|=|ψ>* <ψ|ψ>=1
最後の条件は波動関数の規格化を表しています。 これらを用いてSch.eg.を表すと
H|ψ>=E|ψ>
になります。 また、観測量F(Fに対応する物理量が観測された)に対する期待値は
a=<ψ|F|ψ>
になります。(但し、ψは規格化されている)
![]()
ハミルトニアンが時間に依存しない時、波動関数の時間依存部分を取り除き
それを演算子に負わせて式を簡単にできます。これを ハイゼンベルグ描像といいます。
それに対し、Sch.eg.を用いて解くことはシュレディンガー描像
といいます。
波動関数から時間部分を取り除くには次のようにします。
|ψ(t)>=T|ψo> 但し、T=exp(-iHt/h)
また、演算子Aの期待値も次のようになります。
<ψ(t)|A|ψ(t)>=<ψ(0)|exp(iHt/h)Aexp(-iHt/h)|ψ(0)> =<ψ(0)|AH(t)|ψ(0)> 但し、AH(t)=exp(iHt/h)Aexp(-iHt/h)
という、時間に依存する演算子AHを導入することができます。
dAH(t)= 1 [AH(t),H] dt ih
これは、ハイゼンベルグの運動方程式です。
![]()
極座標表示した波動関数ψ(r,θ,φ)をいきなり解くのは困難です。そこで、
ψ(r,θ,φ)=R(r)Ylm(θ,φ)
のように、r成分とθ,φ成分に分解します。
この、Ylmは球面調和関数といわれ、θとφで決まります。
添え字のl,mは量子状態を決めるもので、lが角運動量,mが磁気量子数
に対応しています。球面調和関数は
Ylm(θ,φ)=(-1)m/(2l+1)(l-m)!\1/2 Plm(cosθ)eimφ \ 4π(l+m)!/
で表されます。ここで、Plm(cosθ)というものが登場しましたが
これは「ルジャンドル陪多項式」というもので直交関数です。そのため
Pl(x)= 1 dl(x2-1)l 2ll!dxl Plm(x)=(1-x2)m/2dmPl(x) dxm ∫-11 PlPmdx= 2δlm δ:デルタ関数 2l+1 Plm(cos(π-θ))=Plm(-cosθ) =(-1)l+mPlm(cosθ)
以上のような関係があります。また、角運動量演算子をLとすると
L2Ylm(θ,φ)=l(l+1)Ylm(θ,φ) l:0,±1,・・・
![]()
先ほどは、球面調和関数を解きました。これは、θ,φに関して解くことができました。
しかし、rに関しても解く必要があります。そこで、ベッセル関数を導入します。
ベッセル関数は、球面調和関数と同じ直交関数です。
また、原点で正則なものを「球ベッセル関数」といい、特徴として
jl(ρ)=/ π \jl+1/2(ρ)=(-ρ)l /1 d \l /sinρ\ \2ρ/ \ρ dρ/ \ ρ /
波動関数を
ψ(r,θ,φ)=R(r)Ylm(θ,φ)
と、分解したときR(r)は
R(r)=(定数)×jl(ρ) 但し、ρ=kr k:波数 k=(2mE/h2)1/2
という関係があります。波数kがあるので、電子の分布は原点を中心として
波のようになっています。これを「球面波」といいます。
以上のように、波動関数ψは同径方向R(r)と角度方向Y(θ,φ)に分解すると
R(r)はベッセル関数で、Y(θ,φ)は球面調和関数として解くことができます。
球ベッセル関数に似ているもので、原点で特異なものを「球ノイマン関数」といいます。
nl(ρ)=(-1)l+1/ π \j-l-1/2(ρ)=-(-ρ)l /1 d \l /cosρ\ \2ρ/ \ρ dρ/ \ ρ /
上記の球ベッセル関数と球ノイマン関数を組み合わせて、ハンケル関数というものがあります。
これには、第1種ハンケル関数と第2種ハンケル関数があります。定義は
hl(1)(ρ)=jl(ρ)+inl(ρ) hl(2)(ρ)=jl(ρ)-inl(ρ)
(1)は添え字のようなもので直接は演算に関係がありません。
今、波動関数ψ(x)があったとします。すると以下のことがいえます。
ψ(x)=cψ(-x) c:定数 =c2ψ(x) ψ(x)=±ψ(-x)
ここで、x→-xの変換を演算子Pで表すと
Pψ(x)=-ψ(x)
です。また
[P,H]=0
で、PとHは交換します。
交換するということは、HとPは同じ固有値を持ちます。
そして、Pの固有値は-1,1です。
このPをパリティ演算子といいます。
空間反転ではx→-xの変換をしましたがt→-tという
時間の反転もあります。時間を反転することで
x→ x x:座標 t→-t t:時間 l→-l l:角運動量
このように、xは変化せず、時間に因子を持っているものだけ
符号が反転します。
![]()
汎関数は関数の関数といったようなものです。 例えば、関数f(x)とg(x)があった場合
g[f]
といったような表記をします。
角運動量は、演算子で表せます。
lx=-i/y∂ -z∂ \ \ ∂z ∂y/ ただし、l=L/hL:角運動量
これは、y,zについてもこのようか関係が成り立ちます。
ただ、ここでlは実際の角運動量Lをhで割ったものであることに注意してください。
これは、lがLie代数になっているからです。Lie代数なので
[lx,ly]=i lz [ly,lz]=i lx [lz,lx]=i ly
という関係があります。また、
l+=lx+ily l-=lx-ily とすると [lz,l±]=±l± [l+,l- ]=2lz
のような関係があります。
いま、l2とlzの同時固有状態を|l,m>で表したとき
l2|l,m>=l(l+1)|l,m> l:整数,反整数(スカラー,ベクトルlの大きさ) lz|l,m>=m|l,m> m:-l・・・l とおいたとき l+|l,m>=((l-m)(l+m+1))1/2|l,m+1> l-|l,m>=((l+m)(l-m+1))1/2|l,m-1>
という公式もあります。
![]()
スピンは、電子の自転によって生じます。
先ほどの角運動量lと区別してsで表します。しかし、本質はlと同様なので
lについて成り立った定理が成り立ちます。
sz|±>=±1/2|±> ただし、s=S/hS:スピン角運動量 |±>=|1/2,±1/2>
ここでもsは実際の角運動量Sをhで割ったものであることに注意してください。
先ほどの公式でl=1/2,m=1/2に相当します。演算子sは行列に対応づけることができて
σ≡2s とすると σx←→/0 1\ σy←→/0 -i\ σz←→/1 0\ \1 0/ \i 0/ \0 -1/ |+>←→/1\ |->←→/0\ \0/ \1/
と、対応づけることができます。この行列を「パウリのスピン行列」といいます。
任意のスピン状態は
|χ>=χ+|+> + χ-|-> ←→ /χ+\ \χ-/
で表せます。
![]()
以上の2つの角運動量を合計は、
J=L+S =(l+s)/h
で表せます。lとsは独立なので、スピンは4l+2通りの状態をとれます。
さて、これを一般的にしてここに2つの波動関数があったとします。
このとき、角運動量は、
J=J1+J2
で表せます。
ただし、このような和は演算子に対してできるもので固有値の和というわけにはいきません。
また、このときの磁気角運動量mはm1+m2というわけにもいきません。
mは次のような表をつくって、範囲を決める必要があります。
| m1\m2 | -j2 | ・ | ・ | j2 |
| -j1 | -(j1+j2) | ・ | ・ | j2-j1 |
| ・ | ・ | ・ | ・ | ・ |
| ・ | ・ | ・ | ・ | ・ |
| j1 | j1-j2 | ・ | ・ | j1+j2 |
mは-(j1+j2)から(j1+j2)の値をとります。
![]()
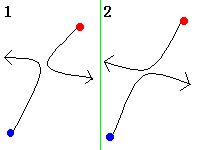 2つの同様な粒子が衝突して跳ね返ったとき
2つの同様な粒子が衝突して跳ね返ったとき
観測者は2粒子の衝突前の進行方向と、
衝突後の進行方向しか観測されません。
古典力学では、2粒子ははっきりを見えるので
1,2のどちらかの衝突が起きたのかわかるのですが
量子力学では、粒子が波の性質があるのでぼやけてしまい
衝突の瞬間は2つの波動関数が重なったようになります。
従って、1,2のどちらの衝突が起きたかはわかりません。
それぞれの原子に番号1,2をつけて、波動関数をψ(1,2)とします。
この原子を交換したときの波動関数をψ(2,1)とすると
ψ(2,1)=±ψ(1,2)
になります。ψ(1,2)のまえに±1がかけられていますが、
+1の時はBose(ボーズ)粒子、-1のときはFermi(フェルミ)粒子
であるということになります。
Bose粒子の例として、陽子、光子などがあります。
Fermi粒子は、電子などがあります。
いま、波動関数が状態μで表せるψμと、ιで表せるψιがあるとする。
両者をあわせた波動関数は
ψ±(1,2)= 1 {ψμ(1)ψι(2)±ψμ(2)ψι(1)} √2 とくに ψ-(1,2)=|ψμ(1) ψμ(2)| |ψι(1) ψι(2)|
後者は「スレーター行列式」といいます。
Fermi粒子は-に、Bose粒子は+にします。
もし、Fermi粒子の場合で、量子状態μとιがひとしいとき、波動関数ψ-(1,2)は
0になってってしまいます。これは、Fermi粒子が同じ状態になれないことを示した
Pauli(パウリ)の排他原理を示しています。
一般にはSch.eg.を厳密に解くのは困難です。
そこで、近似という方法を使います。これは、H=Ho+Vのようにハミルトニアンを
すでに解くことができたHoと、摂動項Vに分けます。
すると、Sch.eg.は、
Hψ=Eψ H=Ho+V
になります。 ここで、Vによる影響がない項について考えると
Hoψn(0)=Eψn(0)
になります。これは、0次摂動項です。意味はVによる項がないということです。
ψ(0)は、ψを0次の摂動項まで考えたということです。この解は
En(0)=εn ψn(0)=un
とおくことにします。
次に、1次の摂動項を考えます。
Hoψn(1)+Vψn(0)=E(0)ψn(1)+E(1)ψn(0) これより En(1)=εn+Vnn ψn(1)=un + ∑ Vkn n(≠k)εn-εk 但し、Vkn=(uk,Vun)
ここで重要なことは、エネルギーの縮退がないということです。
エネルギーの縮体があると波動関数ψnの分数の分母が0になってしまうことがあるからです。
さらに、2次摂動について考えると
Hoψn(2)+Vψn(1)=E(0)ψn(2)+E(1)ψn(1)+E(2)ψn(0) これより En(2)=εn+Vnn+ ∑ |Vmn|2 m(≠n) εn-εm ψn(2)= 省略
2次摂動の波動関数の項を省略したのは式が複雑になるためです。
一般に摂動は、次数が大きくなれば急激に複雑になります。
![]()
縮退がある時は、先ほどの式をそのまま使うことはできません。
ψn(0)=∑bkunk k
のように波動関数の0次の場合を決めます。 それを、
Hoψn(1)+Vψn(0)=E(0)ψn(1)+E(1)ψn(0)
に代入すると、固有値E(1)は
det(N(n)-E(1)1)=| V11(n)-E(1) V12(n) ・・・・・ V1N(n) | | V21(n) V22(n)-E(1) ・・・・・ V2N(n) | | ・・・・・・・・・ | | VN1(n) ・・・・・・・・ VNN(n)-E(1) |
この1は、単位行列のことです。
これから固有値E(1)が求まります。この方程式は「永年方程式」といいます。
![]()
今までは、定常状態でのSch.egの摂動を求めたのですが、ここでは、時間に依存する場合を考えます。
ψo(t)=∑anφn(t) 但し、φn(t)=exp(-iεn t/h)un
のように波動関数の0次の場合を決めます。akに関しては
ih∂ak(t)=λ∑ Vkn(t) exp(iωknt)an(t) ∂t n
から、求めることができます。
![]()
摂動論で使った方法は摂動項が小さい場合にしか使えません。
また、摂動項は複雑になってしまいます。
そこで、もっとかんかんな方法として変分法があります。
これは、関数の最大(最小)値を求めるときに微分したのと同じです。
但し、厳密には求まりません。
例えば、関数E(a)の最小値を求めるのに
∂E(a) =0 ∂ a
をみたすようなaが求まります。
しかし、E(a)は本当の最小値よりは大きくなります。(小さくなることはありませんが)
従って、参考程度に考えた方がいいようです。
![]()
量子力学では、軌道角運動量が
J=0h,1h,2h・・・
と量子化されていました。古典力学では、
h=0
になっているので、角運動量は連続的に値をとることができます。
これを、Sch.eg.についても適用することができます。
ψ=exp(iS/h) S=S(r,t) として ih∂ψ = Hψ ∂t に代入し、テーラー展開して第1項を求め、h=0とすると -∂S(0) = H ∂t
最後の式は「ハミルトン・ヤコビーの方程式」の形になっているので
古典力学の式に変形できました。
(S(0)はSの0次の近似)
コラム 「TEX」TEXというパソコンソフトをご存じでしょうか? これは、パソコンで数学的な記号をちゃんと表そうをして、ある数学者が 現代のバージョンは、Ver3.1415です。 |