![]()
![]()
| 侾丆惷巭棳懱 | 楢懕懱偲偼丂椡丂峫偊曽丂棳慄丂塓搙丂棳傟娭悢丂棳懱偺庬椶 |
| 俀丆姰慡棳懱 | 僆僀儔乕偺塣摦曽掱幃丂儀儖僰乕僀丂埑椡丂棳慄嬋棪 |
| 俁丆傂偢傒偲墳椡 | 傂偢傒丂墳椡丂僯儏乕僩儞棳懱偱偺墳椡丂偮傝崌偄偺幃 |
| 係丆旕埑弅惈棳懱偺椡妛 | 俶亅俽曽掱幃丂楢懕偺幃丂塣摦検偺棳傟丂儗僀僲儖僘丒僗僩儖乕僴儖 |
楢懕懱偼丄婥懱傗抏惈懱丄擲惈懱偺傛偆偵曄宍偡傞傕偺傪庢傝埖偄傑偡丅
旝彮懱愊偺晹暘傕埖偆偺偱偡偑丄暘巕偺儗儀儖傑偱偼峴偒傑偣傫丅
偣偄偤偄侾兪倣掱搙偱偡丅偙傟傪夝偔偵偼丄師偺俁偮偺曽掱幃傪巊偄傑偡丅
丒婎慴曽掱幃
丒塣摦偺朄懃
丒峔惉曽掱幃
戞俀幃偲俁幃偼旕慄宍側偨傔丄們倎倧倱揑側尰徾偑偁傝傑偡丅
![]()
棳懱偵摥偔椡偼丄師偺懱愊椡偲柺愊椡偲偺偮傝崌偄偱昞偡偙偲偑偱偒傑偡丅
暔懱偺懱愊偵斾椺偟偰摥偔椡偱偡丅
嬶懱揑側椺偲偟偰晜椡側偳偱偡丅
俥亖兿俲嚈倁丂丂丂丂丂兿丗枾搙 丂丂丂丂丂丂丂丂丂丂丂俲丗扨埵幙検偁偨傝偺奜椡 丂丂丂丂丂丂丂丂丂丂嚈倁丗旝彮懱愊
偙傟偼埑椡倫傪巊偭偰傕昞偣傑偡丅
俥亖亅佫倫嚈倁
暔懱偺柺愊偵斾椺偟偰摥偔椡偱偡丅
嬶懱揑側椺偲偟偰婥埑丒悈埑側偳偱偡丅
俥亖俹嚈俽丂丂丂丂丂丂俹丗埑椡 丂丂丂丂丂丂丂丂丂丂嚈俽丗旝彮柺愊
埲忋偺幃傪僀僐乕儖偱寢傇偙偲偵傛偭偰偮傝崌偄偺幃偑偱偒傑偡丅
兿俲丂亖丂佫俹
![]()
棳懱傪峫偊傞偵偼丄師偺俀捠傝偑偁傝傑偡丅
偙傟偼丄侾偮偺棻巕傪偳偙偐傜偳偺傛偆偵堏摦偟偰偄偔偐傪捛愓偡傞曽朄偱偡丅
偙傟偼丄棻巕偑侾侽23傕偁傞偲捛愓偡傞偺偑傎偲傫偳晄壜擻偱偡丅
偙傟偼丄摿掕偺応強偺棻巕偺悢傪娤應偡傞曽朄偱偡丅
棳懱偱偼偙偪傜偺曽朄傪懡梡偟傑偡丅
暔懱偺埵抲傪乮倶丆倷丆倸乯
懍搙傪丂倴亖乮倳丆倴丆冎乯丂偱偁偨偊傑偡丅
暔棟検乮埵抲丆懍搙丆埑椡側偳乯傪俥偱偁傜傢偡偲
嚈俥亖乛佪丂丂亄丂倴丒佫乢丂俥 嚈倲丂乢佪倲丂丂丂丂丂丂乛
偙傟傪暔幙旝暘乮儔僌儔儞僕儏旝暘乯偲偄偄傑偡丅
![]()
棳慄偲偼丄帪娫偺奺弖娫偛偲偺棳傟偺愙慄儀僋僩儖偺偙偲偱偡丅
崱丄(x,y,z)幉曽岦偺懍搙傪(u,v,冎)偲偡傞偲丄
倓倶亖倓倷亖倓倸 倳丂丂倴丂丂冎
偲偄偆旝暘曽掱幃偑惉傝棫偪傑偡丅
![]()
愭傎偳偺懍搙丗(u,v,冎)亖倴丂偲偡傞偲丄
冎亖倰倧倲 倴
偲丄偁傜傢偣傑偡丅
![]()
俀師尦棳偱乮侾偮偺幉曽岦偺棳傟偑側偄乯丄旕埑弅棳懱偺偲偒
佪倳亄佪倴亖侽 佪倶丂佪倷
偲偄偆娭學偑偁傝傑偡丅偙偙偱棳傟娭悢傪掕媊偡傞偲師偺傛偆偵傕彂偗傑偡丅
倳亖佪冋丂倴亖亅佪冋 丂丂佪倷丂丂丂丂佪倶丂丂偲偡傞偲 倓冋亖倳倓倷亅倴倓倶
偙偺冋傪棳傟娭悢偲偄偄傑偡丅傑偨塓搙偼
冎亖丂丂乛佪2冋丂亄丂佪2冋乢 丂丂丂丂乢佪倶2丂丂丂佪倷2乛
偲側傝傑偡丅
![]()
棳懱傪暔棟揑偵夝偔偵偼丄擲惈丄埑弅側偳傪峫偊側偔偰偼側傜偢擄夝偱偡丅
偦偙偱棳懱傪嬤帡偟偰幃傪夝偙偆偲偟傑偟偨丅埲壓偼棳懱偺柤徧偱偡丅
惷巭偟偨棳懱偺偙偲偱偡丅
惷巭偟偰偄傞偨傔椡妛揑側僄僱儖僊乕偼懱愊椡丄柺愊椡丄億僥儞僔儍儖側偳偟偐側偔
擲惈偵傛傞塭嬁丄杸嶤側偳偑偁傝傑偣傫丅
姰慡棳懱偲偼丄擲惈偑侽偺棳懱偺偙偲偱偡丅
擲惈偑侽側偺偱棳傟偵暯峴側柺偵偼杸嶤偑偁傝傑偣傫丅
棳懱偺枾搙偑帪娫丄応強偵傛傜偢堦掕側棳懱偺偙偲偱偡丅
棳懱偺枾搙偑帪娫丄応強偵傛偭偰曄壔偡傞棳懱偺偙偲偱偡丅
埑弅惈棳懱偺堦庬偱偡丅偨偩丄枾搙偑幃偱昞偡偙偲偑偱偒丄
兿亖f(倫)丂丂丂丂倫丗埑椡丂丂兿丗棳懱偺枾搙
偙偺傛偆偵棳懱偺枾搙偑埑椡倫偺傒偵傛偭偰寛傑傞傕偺偱偡丅
懍搙岡攝偑堦掕側棳懱偱偡丅廬偭偰丄懍搙傪倳偲偡傞偲
倓倳亖const 倓倶
偵側傝傑偡丅娗偺拞偵棳懱偑偁傞偲暻晅嬤偱偼懍搙偼侽側偺偱偡偑
暻偐傜偺嫍棧偵斾椺偟偰棳懍偑憗偔側傝傑偡丅
姰慡棳懱偲偼丄擲惈偑侽偺棳懱偺偙偲偱偡丅
姰慡棳懱偲偼擲惈偑側偄偨傔丄懍偝偺堘偆俀偮偺棳懱偑愙偟偰偄偰傕
偍屳偄偵椡傪媦傏偟偁偆偙偲偑偁傝傑偣傫丅乮恑峴曽岦偵懳偟偰乯
僆僀儔乕偺塣摦曽掱幃偼姰慡棳懱偵懳偡傞塣摦曽掱幃偱丄乽偮傝崌偄偺幃乿偲
俥亖倣倎偲偄偆娭學傪梡偄偰偄傑偡丅
俢倴亖亅侾佫倫丂亄丂俲 俢倲丂丂兿
偙偙偱丄倫偼埑椡丄倴偼棳懱偺懍搙丄俢偼旝暘偺婰崋偱偡丅
側偤丄倓偲偄偆旝暘婰崋傪梡偄側偄偺偐偲偄偆偲丄悢妛揑偵
惓偟偄旝暘偱偼側偄偐傜偱偡丅
![]()
俫亖侾倴2丂亄丂俹丂亄丂兌丂丂丂兌丗億僥儞僔儍儖丂丂俹丗埑椡娭悢 丂丂俀 俹亖佺倓倫乛兿
偙偺俫傪儀儖僰乕僀娭悢偲偄偄傑偡丅
幚偼丄塃曈偵幙検倣傪偐偗傞偲乽僄僱儖僊乕曐懚偺幃乿偵側偭偰偄傑偡丅
掕忢側棳懱偼俫傪堦掕偵曐偮傛偆側棳傟傪偟傑偡丅乮儀儖僰乕僀偺掕棟乯
![]()
棳慄偺暘婒偲偄偆偺偼偁傝摼傑偣傫丅廬偭偰暘婒偟偰偄傞偲偄偆偺偼
懍搙偑侽偱偁傞偲偄偊傑偡丅偦偺揰偺偙偲偼乽傛偳傒揰乿偲偄偄傑偡丅
偙傟偼丄棳懱偑惷巭暔懱偵偁偨傝傛偗傞偲偒偵敪惗偟傑偡丅
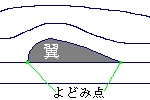
傛偳傒揰偵偐偐傞埑椡傪憤埑丄尦乆偁傞埑椡傪惷埑丄棳傟偵傛偭偰敪惗偡傞埑椡傪
摦埑偲偄偭偰埲壓偺娭學偑偁傝傑偡丅
倫丂亄丂侾兿倴2丂亖倫o 丂丂丂丂俀
嵍曈戞侾崁偑惷埑丄俀崁偑摦埑丄塃曈偑憤埑偱偡丅
![]()
棳慄偑嬋偑偭偰偄傞偲偒偵偼丄埲壓偺娭學偑偁傝傑偡丅
侾佪倯2亖亅侾佪倫 俀佪倱 丂丂兿佪倱 兿倯2亖亅佪倫 丂俼 丂丂佪値
偙傟傜偺幃傪棳慄嬋棪偺掕棟偲偄偄傑偡丅
偙偙偱丄倯偼棳慄偺懍搙丄兿偼棳懱偺枾搙丂傑偨丄棳傟偵悈暯側惉暘傪倱丆悅捈側惉暘傪値偲偟偰偄傑偡丅
俼偼棳懱偺棳傟傪墌偵嬤帡偟偨偲偒偺敿宎偱偡丅
偦偺偙偲偐傜丄媫側墌偱偁傞傎偳埑椡偑尭彮偟傑偡丅偙傟傪墳梡偟偨偺偑旘峴婡偱偡丅

旘峴婡偼丄壓偺曽偼悈暯偵側偭偰偄傑偡丅偟偐偟丄忋偺曽偼
娵傒傪懷傃偰偄傑偡丅偙傟偼墌偵嬤帡偱偒傞偺偱丄愭傎偳偺掕棟偐傜
埑椡偑尭彮偟傑偡丅廬偭偰旘傇偺偱偡丅
旝彫側棻巕偑棳傟傞偲偒俁偮偺曄宍傪偟偰偄傑偡丅偦傟偼丄
偙偺俁偮偑偁傝傑偡丅偙偺偲偒曄埵傪倱偱昞偡偲僥乕儔乕揥奐偱偒偰丄
倱i亖倱io亄乛佪倱i乢倶j丂亄丂丒丒丒丂丂乮i,j伕侾丆俀丆俁乯 丂丂丂丂丂 乢佪倶j乛
偙偺塃曈戞俀崁偺旝暘晹暘偼僥儞僜儖偱昞帵偱偒傑偡丅
僥儞僜儖偼丄懳徾僥儞僜儖偲旕懳徧僥儞僜儖偵暘夝偱偒傑偡丅
乛兠11丂兠12丂兠13乢 丂丂兠ij亖侾乛佪倱i亄佪倱j乢 乥 兠12丂兠22丂兠23 乥丂丂丂丂丂俀乢佪倶j丂佪倶i乛 乢兠13丂兠23丂兠33乛 丂丂兠ij丗庡傂偢傒 乛丂侽丂丂丂冇12丂冇13乢 丂丂冇ij亖侾乛佪倱i亅佪倱j乢 乥 亅冇12丂丂侽丂丂冇23 乥丂丂丂丂丂俀乢佪倶j丂佪倶i乛 乢亅冇13丂亅冇23丂侽丂乛
庡傂偢傒偼嵗昗曄姺偵傛偭偰
乛兠1丂侽丂侽乢 乥 侽丂兠2丂侽 乥 乢侽丂 侽 兠3乛
偝傜偵僩儗乕僗偼嵗昗曄姺偵懳偟晄曄側偺偱
兠1亄兠2亄兠3亖兠11亄兠22亄兠33亖div 倱
偵側傝傑偡丅偙偺倓倝倴 倱偼嚈倁乛倁偵摍偟偔丄乽懱愊傂偢傒乿偲偄偄傑偡丅
![]()
墳椡偲偼丄扨埵柺愊摉偨傝偵偐偐傞椡偺偙偲偱偡丅
乛俿1乢 丂乛冄11丂冄12丂冄13乢 乛値1乢 乥 俿2 乥亖乥 冄21丂冄22丂冄23 乥乥 値2 乥 乢俿3乛 丂乢冄31丂冄32丂冄33乛 乢値3乛
偱偁傜傢偟傑偡丅偙偙偱丄冄ii偼乽朄慄墳椡乿丄冄ij(i亗j)偼乽愙慄墳椡乿偲偄偄傑偡丅
偙傟傕丄嵗昗曄姺偵傛偭偰懳妏宍偵偱偒傑偡丅
乛冄1丂侽丂侽乢 乥 侽丂冄2丂侽 乥 乢侽丂 侽 冄3乛
旕埑弅惈棳懱拞偱偼丄墳椡僥儞僜儖偼師偺傛偆偵媮傑傝傑偡丅
冄ij亖乮亅倫 亄 內 div 倴乯兟ij丂亄丂俀兣倕ij 偨偩偟丄 倕ij亖佪兠ij丂丂丂丂丂丂內丗暔幙掕悢 丂丂丂佪倲
僯儏乕僩儞棳懱拞偱偼
冄xy亖兣倓倳丂丂丂丂丂倳丗倶曽岦偺懍搙 丂丂丂丂倓倷
![]()
僯儏乕僩儞棳懱偱偼埲壓偺墳椡僥儞僜儖偑惉傝棫偭偰偄傑偡丅乮旕埑弅棳懱偱乯
乛冄11丂冄12丂冄13乢 丂 乛亅倫亄俀兣倕11丂丂俀兣倕12丂丂丂丂俀兣倕13丂丂乢 乥 冄21丂冄22丂冄23 乥亖乥 丂俀兣倕21丂丂丂亅倫亄俀兣倕22丂丂俀兣倕23 丂丂乥 乢冄31丂冄32丂冄33乛 丂 乢丂俀兣倕31丂丂丂丂俀兣倕32丂丂丂亅倫亄俀兣倕33乛 兣丗擲惈棪丂丂倕ij丗扨埵儀僋僩儖乮i曽岦偺柺偑j曽岦偵墴偝傟傞椡乯
埲壓偵擲惈棪偺抣傪帵偟傑偡丅
| 暔懱 | 擲惈棪 |
| 嬻婥乮俀侽搙乯 | 侾丏俉侾亊侾侽-5 |
| 嬻婥乮侽搙乯 | 侾丏俈侾亊侾侽-5 |
| 悈乮俀侽搙乯 | 侾丏侽侽亊侾侽-3 |
| 悈乮侽搙乯 | 侾丏俈俋亊侾侽-3 |
偙傟偐傜丄壏搙偵傛偭偰擲惈棪偑曄傢傞偙偲偑傢偐傝傑偡丅
![]()
埲慜丄偮傝崌偄偺幃
兿俲丂亖丂佫俹
偲偄偆偺傪徯夘偟傑偟偨偑墳椡冄傪巊偭偰傕偙偺幃傪昞偣傑偡丅
佪冄ij丂亄丂兿俲i亖侽 佪倶j
晞崋偑媡偵側偭偰偄傑偡偑偙傟偼丄埑椡儀僋僩儖倫偼暔懱偐傜尒傞偲
斀懳偵椡傪庴偗傞偨傔偱偡丅
旕埑弅惈棳懱偲偼枾搙偑忢偵堦掕偺棳懱偺偙偲偱偡丅
僫價僄乕僗僩乕僋僗曽掱幃傪棯偟偰俶亅俽曽掱幃偲偄偄傑偡丅
埲壓偼丄旕埑弅惈棳懱偺塣摦曽掱幃偱偡丅
佪倴亄乮倴丒佫乯倴亖亅侾佫倫亄兯嚈倴亄俲 佪倲丂丂丂丂丂丂丂丂丂兿 丂丂丂丂丂兿丗枾搙丂丂丂俲丗懱愊椡丂丂兯丗塣摦擲惈棪 兯亖兣丂丂兣丗乮惷巭乯擲惈棪 丂丂兿
嵍曈戞侾崁偼旕掕忢崁丄戞俀崁偼堏棳崁丄塃曈戞侾崁偼埑椡崁丄戞俀崁偼擲惈崁偱偡丅
嵍曈傪傑偲傔偰姷惈崁偲偄偭偨傝傕偟傑偡丅
偙傟偼丄僆僀儔乕偺曽掱幃
俢倴亖亅侾佫倫丂亄丂俲 俢倲丂丂兿
傪奼挘偟偨傕偺偱偡丅
扨埵懱愊偁偨傝偺椡俲偼丄廋惓埑椡倫*傪
倫*亖倫亄兿兌丂丂丂兿丗枾搙丂丂兌丗億僥儞僔儍儖
偲掕媊偟丄俶亅俽曽掱幃偵戙擖偡傞偲懱愊椡俲偑徣棯偱偒傑偡丅
擲惈棪偼丄惷巭偟偰偄傞偲偒偲摦偄偰偄傞偲偒偱偼埲壓偺傛偆偵堘偭偰偒傑偡丅
| 暔懱 | 乮惷巭乯擲惈棪 | 塣摦擲惈棪 |
| 嬻婥 | 侾丏俉侾亊侾侽-5 | 侾丏俆侽亊侾侽-5 |
| 悈 | 侾丏侽侽亊侾侽-3 | 侾丏侽侽亊侾侽-6 |
| 僌儕僙儕儞 | 侾丏俆侽 | 侾丏侾俉亊侾侽-3 |
傑偨丄
俼倕亖乮堏棳崁乯丂丂丂丂丂俽倲亖乮旕掕忢崁乯 丂丂丂乮擲惈崁乯丂丂丂丂丂丂丂丂乮堏棳崁乯
偲掕媊偟偰丄俼倕偼乽儗僀僲儖僘悢乿丄俽倲偼乽僗僩儖乕僴儖悢乿偲偄偄傑偡丅
俼倕偼丄戝偒偗傟偽擲惈偑彮側偄偙偲傪堄枴偟傑偡丅
俽倲偼棳懱偺帪娫埶懚惈傪堄枴偟丄掕忢棳偺帪偼俽倲亖侽偵側傝傑偡丅
![]()
棳懱偼傢偒弌偟偨傝徚柵偡傞偲偄偭偨偙偲偑偁傝傑偣傫丅
偮傑傝丄楢懕偱偁傞昁梫偑偁傝傑偡丅偦偙偱師偺幃偑惉傝棫偪傑偡丅
佪兿亄倓倝倴乮兿倴乯亖侽 佪倲
偙傟偑乽楢懕偺幃乿偲偄偆傕偺偱偡丅
旕埑弅惈棳懱偺栤戣偼丄楢懕偺幃偲俶亅俽曽掱幃傪楢棫偝偣偰夝偒傑偡丅
![]()
棳懱拞偵椞堟倁傪偲傝傑偡丅倁偑庴偗傞椡偼柺愊椡丄懱愊椡
偦偟偰扨埵帪娫偵棳擖偡傞塣摦検偱偡丅
旝彮柺愊倓俽傪捠偟偰棳擖偡傞塣摦検偼俧倓俽偱偡丅俧偼
俧亖倫値丂亄丂兿倴倴n丂丂丂
俧偼乽塣摦検偺棳傟枾搙乿偲偄偄傑偡丅偙傟偼丄塣摦検偲摨偠傛偆側傕偺偱偡丅
俫亖倶 亊 俧
俫偼乽妏塣摦検偺棳傟枾搙乿偱偡丅
![]()
挿偝丄帪娫丄懍搙偺扨埵傪帩偮傕偺偲偟偰俴丆俿丆倀傪慖傫偩偲偒
俼倕亖倀俴丂丂丂兯丗擲惈棪 丂丂丂 兯 俽倲亖 俴 丂丂丂倀俿
偙偺傛偆偵儗僀僲儖僘悢俼倕偲丄僗僩儖乕僴儖悢俽倲偑掕媊偱偒傑偡丅
俼倕偺扨埵偺師尦偲偟偰
俼倕佸丂(堏棳崁) 丂丂丂丂(擲惈崁)
俽倲偺扨埵偺師尦偲偟偰
俽倲佸丂(旕掕忢崁) 丂丂丂丂 (堏棳崁)