![]()
![]()
| �P�C�M�͊w�̑�P�@�� | ��ԕ������@�t�@���f�����[���X�@�M�͊w��P�@���@�ϕ��@�f�M�ω� |
| �Q�C�M�͊w�̑�Q�@�� | �N���E�W�E�X�̕s�����M�͊w��Q�@���@�w�����z���c�@�M�u�X�@���w�|�e���V���� |
| �R�C���q�^���_ | ���z���@���x�@��M�@�G���S�[�h�����@�z�u���@�G�l���M�[�@�����W�c |
�@�@�@�@�@�@�@�@�o�F���́@�@�@�u�F�̐� �o�u�����q�s�@�@���F���q�̐��@�s�F���x
�����Œ��ӂ��Ăق����̂́A���w�̋C�̂Ɋւ���������Ǝ��Ă���̂ł����P�ʂ��Ⴄ�Ƃ������Ƃł��B
�Ⴆ�o�ł����A���w�ł͂o [atm]�Ƃ����܂����B
�Ƃ��낪�����ł́A�o�@[�m�^��2]�Ƃ����P�ʂɂȂ�܂��B
�ȉ��ɂ��̈Ⴂ���܂Ƃ߂Ă݂܂����B
| �@ | ���� | ���w |
| �o�i���́j | �m�^��2 | ������ |
| ���i�ʁj | ������ | ������ |
| �s�i���x�j | �j | �j |
| �q�i�C�̒萔�j | �W�D�R�P | �O�D�O�W�Q |
���̎��́A���z�C�̂ɐ��藧���܂��B
���z�C�̂Ƃ́A�C�̕��q�̑̐ς��O�ŁA���q���m�̑��ݍ�p���Ȃ����̂ł��B
�����ŁA�{���c�}���萔��
��B���@�q�@ �@�@�@�mA
�ƒ�`����ƁA�C�̂̏�ԕ�������
�o�u���m ��B �s
�����ŁA�m�͋C�̂̕��q�̐��ł��B
![]()
��قǂ̎��͎��ۂ̋C�̂Ƒ�������Ă��܂��B����͎��ۂɂ́A���q�Ԃ̑��ݍ�p������
�C�̕��q�̑傫�������邩��ł��B�����̈��q�������ꂽ�̂����̎��ł��B
�^�o �{ �� ��2�_�i�u�|�����j�����q�s
�_�@�@ �u2�@�^
�����ŁA�o�C�u�C�s�C�q�C���́A��قǂ̒ʂ�ł��B���C���͒萔�ŁA�������ƂɌ��܂��Ă��܂��B
���̎��͔��ɂ悭�ł��Ă��āA�C�̂����ł͂Ȃ��t�̂ɂ��K�p�ł��܂��B
���̎����A�t�@���f�����[���X�̎��Ƃ����܂��B
���̎��������ƁA�ȉ��̂悤�Ȃ��тꂪ�ł��܂��B�i�ł��Ȃ��Ƃ�������܂��B�j
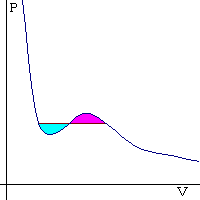
������͐}�̋Ȑ��̂悤�ɓ�����܂����A���ۂ͐}�̎��Ɛ��F�̖ʐς������ɂȂ�悤��
�����������܂��B���̋�Ԃ̉��x�ω��͐����ɂȂ�܂��B
���̂Ƃ��A�t�̂ƋC�̂̕ω��������܂��B
![]()
���t���|�����u�@�{�@���f�p�@�@�t�F�����G�l���M�[�@�p�F�M��
���ꂪ�A�M�͊w��P�@���ł��B���f�p�́A���w�I�ɂ͔����͂ł��Ȃ��̂Łu�f�i�v���C���j�v
�����܂��B�ȉ��̎��͂悭�g�����������܂����B�i����Ȃ��ȂƎv���Č��Ă��������B�j
�t���t(T,V)�@�Ȃ̂�
���t���^�݂t�_�@ �{�@�^�݂t�_
�@�@�@�_�݂s�^V�@�@�@�_�݂u�^T
���f�p���^�݂t�_ ���s�{�^���{�^�݂t�_ �_���u�@�@�@�|�|�|�|�|�|�@
�@�@�@�@�_�݂s�^V�@�@�@�_�@�@�_�݂u�^T�^
��M�bv���^�݂t�_
�@�@�@ �@�_�݂s�^V
�@����舳��M���l����B�@�S�̂����s�ł���
�^�݂t�_�@�{�@�^���{�^�݂t�_ �_ �^�݂u�_�@�����f�p�@���@�bp
�_�݂s�^V �@�@�_�@�@�_�݂u�^T�^ �_�݂s�^p �@���@�s
�^�݂t�_�@�͒�ϔ�M�bV��\���Ă��܂��B�܂��A���z�C�̂ł́A
�_�݂s�^V
�^�݂t�_�@���O�@�ɂȂ��Ă���̂�
�_�݂u�^T
���u���q�s�Ƃ����W����
�bp���bv�@�{�@���^�݂u�_�@���bv�@�{�@�q
�@�@ �@�@�@�@�@ �_�݂s�^p
�Ō�̎��́A�u�}�C���[�̊W�v�Ƃ����܂��B
![]()
�M���v�ł͕ϕ��𑽗p���܂��B
���͂����s�Ƃu�̊��ł���Ƃ������Ƃ���Ō�̎��̂悤�Ȃ��ꂢ�Ȍ`�ɂȂ�܂��B
������(�s�C�u)���
�������^�݂��_���s�@�{�@�^�݂��_���u
�@�@�@�_�݂s�^V �@�@�@�@�_�݂s�^T
�������̎��������O�A�����đS�̂����s�Ŋ����
�^�݂��_�@�{�@�^�݂��_ �^���u�_�@���O�@�@�@�|�|�|�|�|�|�@
�_�݂s�^V �@�@�_�݂u�^T�_���s�^p
�����
�^�݂��_ �^�݂s�_�@���P�@�@�@�@�@�@�@�@�@�@�|�|�|�|�|�|�A
�_�݂s�^V�_�݂��^V�@�@�@�@�@�@�Ȃ̂�
�@��(�݂s�^�݂�)V��������Ƒ�P�����A�̊W����P�ɂȂ�̂�
�^�݂s�_ �^�݂��_ �^���u�_�@���@�|�P�@�@�@ �|�|�|�|�|�|�B
�_�݂��^V�_�݂u�^T�_���s�^p
�S�����̂Ƃ��́A�A�̊W�͂����܂����B�ϔ����̎��͉������ɂ���̂�
�Ƃ����̂��d�v�ɂȂ�܂��B�A��V�����ɂ��܂����B
�B�͈��ɂ�����̂����ꂼ��̍��ňقȂ�̂Ł@(�E��)���P�@�Ƃ������Ƃ�����܂���B
�ȉ��͕ϕ��ŏd������ł��B�������A���C���C���C�ւ͓Ɨ��ϐ��ł��B
�^�݂��_ ���^�݂��_-1
�_�݂��^z�@�_�݂��^z
�^�݂��_ ���^�݂��_ �^�݃��_
�_�݂��^z�@�_�݃ց^z�_�݂��^z
�^�݁@�_ �^�݃��_ ���^�݁@�_ �^�݃��_
�_�݂��^y�_�݂��^z�@�_�݂��^x�_�݂��^z
�^�݂��_ ���|�^�݂��_ �^�݂��_
�_�݂��^z�@�@�_�݂��^y�_�݂��^x
�^�݃��_ ���^�݃��_ �{�^�݃��_ �^�݂��_
�_�݂��^x�@�_�݂��^z�@�_�݂��^y�_�݂��^x
�ォ��Q�Ԗڂ̎����uchain�@rule�v�A�R�Ԗڂ��uMaxwell�@rule�v�Ƃ����܂��B
�B���͎��͂S�Ԗڂ̎����Ƃ������Ƃ��킩��܂��B
![]()
�^�݂t�_�@�{�@�^���{�^�݂t�_ �_ �^�݂u�_�@���O�@�i��f�M�ω���肄�f�p���O�j
�_�݂s�^V �@�@�_�@�@�_�݂u�^T�^ �_�݂s�^p
���z�C�̂�z�肵�āA�bv�����A(�݂t�^�݂u)T���O�@�Ƃ����
�bv ���s�@�{�@�� ���u�@���O
�P�������ɂ��čl���A���u���q�s�����A�S�̂��s�Ŋ����
�bv ���s�@�{�@�q ���u�@���O
�@�@�s�@�@�@�@�@ �u
�q���bp�|�bv�@�����bp�^�bv�@���
���s�@�{�@(���|�P)���u�@���@�O�@�@�����ϕ������
�s�@�@�@�@�@�@�@�@�u
�s �u��-1������������
���u��������������
�Ƃ����������܂�܂��B���͕������Ƃ̂bv�A�bp�Ō��܂�܂��B
�P���q�̂Ƃ��̓����T�^�R�A�Q���q���q�̂Ƃ��̓����V�^�T�ɂȂ�܂��B
��ԕϐ��r��
���f�p�����r �@�s
�Œ�`����Ă��܂��B����������́A�t�ω��̏ꍇ�ł��B
�s�t�ω��̏ꍇ�A����T�C�N�������Ă�������Ԃɖ߂�܂���B
���̂Ƃ��̎���
���f�p�����r �@�s
�ɂȂ�܂��B
![]()
�M�͊w��Q�@���́A�s�t�ߒ��ɂ��ďq�ׂĂ��܂��B
����́A�ቷ�M�����獂���M���ɔM���ړ����Ȃ��Ƃ��������Ƃł��B
�����ŁA��ԕϐ��r�Ƃ����̂�����܂��B
���f�p���s ���r
���t���|�� ���u �{ ���f�p�@�@�@�@�@�ȏォ��
���t���|�� ���u�@�{�@�s ���r
���r�������u�@�{�@���t
�@�@�@�@�s�@�@�@�@ �s
�@�@�����q���u�@�{�@���bv���s�@�@�@�ϕ������
�@�@�@�@�u�@�@�@�@�@�@�@�s
�r�����bv �����s�@�{�@���q �����u�@�{�@�ro
���̂悤�ɕ\���܂��B�r�̓G���g���s�[�Ƃ������܂��B
�s�t�ߒ��ł́A����T�C�N���ł��A�G���g���s�[�����債�܂��B
������u�G���g���s�[����̖@���v�Ƃ����܂��B
![]()
�w�����z���c�͎��̂悤�ȔM�͊w�����`���܂����B
�e���t�|�s�r
����́A�Ɨ��ϐ����s�C�u�ɂ��Ă���̂ŁA�s�C�u���킩���Ă���Ƃ��ɕ֗��ł��B
���e���|�r ���s�|�� ���u�@�@������ �r���|�^�݂e�_ �@�@�@�_�݂s�^V �����|�^�݂e�_ �@�@�@�_�݂u�^T�@�@�ȏ�̂Q������ �^�݂r�_�@���^�݂��_ �_�݂u�^T �@�_�݂s�^V
�Ō�̎����u�}�N�X�E�F���̊W���v�Ƃ����܂��B
�s���r�����f�p
���t���|�����u�@�{�@���f�p�@�@�ȏ�̊W����
�s ���r�|���t�|�� ���u���O
���C�u�����̂Ƃ���
��(�s�r�|�t)���O
���e���O
������A���t�̏����͂s�C�u�����̂Ƃ��A�e���ɏ��̂Ƃ��ł��B
![]()
�M�u�X�͎��̂悤�ȔM�͊w�����`���܂����B
�f���t�|�s�r�{���u
����́A�Ɨ��ϐ����s�C�o�ɂ��Ă���̂ŁA�s�C�����킩���Ă���Ƃ��ɕ֗��ł��B
���f���|�r ���s�{�u �����@�@������
�r���|�^�݂f�_
�@�@�@�_�݂s�^p
�u���^�݂f�_
�@�@�_�݂��^T�@�@�ȏ�̂Q������
�^�݂r�_�@���|�^�݂u�_
�_�݂��^T �@�@�_�݂s�^p
�Ō�̎����u�}�N�X�E�F���̊W���v�Ƃ����܂��B
��قǂƓ���������
�s ���r�|���t�|�� ���u���O ���C�s�����̂Ƃ��� ��(�s�r�|�t�|���u)���O ���f���O
���t�̏����́A�s�C�������̂Ƃ��A�f���ɏ��̂Ƃ��ł��B
![]()
����́A�P���q�ɂ��G�l���M�[�����݂���Ƃ��������̂ł��B
���t���|�����u�@�{�@�s���r�@�{�@����j ���mj
�ʂ͎��̂悤�ɂ��ċ��܂�܂��B
��j���|�s�^�݂r �_�@�@�@�@�@���^�݂e �_�@�@�@�@���^�݂f �_ �@ �@�@�@�_�݂mj�^U,V,(Nj)�@�@�_�݂mj�^T,V,(Nj)�@�_�݂mj�^T,p,(Nj)
������(Nj)�Ƃ����̂͂m�������ȊO�����ɂ���Ƃ������̂ł��B
�M���v�̐��E�ŏd�v�Ȃ͎̂��̎��ł��B
��(v)�������m�^�@�@���@ �_3/2 �������i�|����2�^�Q��B�s�j���� �@�@�@�@�@ �@�_�Q��B�s�^
����́A���x�������炖�{�����ɑ��݂��闱�q�̐��ł��B
�S�̂��m�Ŋ���P���q�����`���{�����ɑ��݂���m���ɂȂ�܂��B
��B�́u�{���c�}���萔�v�Ƃ������̂ł��B
�@�������i�|�Á^��B�s�j�@�@�@�Á�����2�^�Q ���������i�|�Ã��j�@�@�@�@�@ �����P�^��B�s
�́A�u�{���c�}�����q�v�Ƃ������̂ŁA��قǂ̎��ɂ����̈��q������܂��B
![]()
�C�̕��q�̑��x�͎��̂悤�ɋ��܂�܂��B
����p�����@�Q�@���^���{�R�_�@�^�Q��B�s�_
�@�@�@�@��1/2�@ �_�@�Q�@�^�@�_�@���@ �^
����p���͑��x����p�̑��x�̕��ϒl�ł��B
�Ⴆ�A��2�̕��ϒl�͂����Q�Ƃ�������̂ł��B
���̓K���}���Ƃ������̂ŁA���̂悤�Ȑ���������܂��B
���i���{�P�j�������i���j
���i���j���i���|�P�j�I
���i�P�^�Q�j��(��)1/2
![]()
�G�l���M�[�͂P���R�x�����邽�тɂP���q�����肋B�s�^�Q���������܂��B
�]���āA���R�x������������ƂP������������
�t�����q�s�@�@�@�@�q�F�C�̒萔
�@�@�@�Q
�bv�����q�@�@�@�@ ���F���R�x
�@�@�@�Q
�bp��(���{�Q)�q
�@�@�@�Q
�������{�Q
�@�@�@��
�Ⴆ�A�P���q���q�̂Ƃ��́A���R�x��x,y,z����������̂Ŏ��R�x�����R�ł��B
�Q���q���q�ł́A���̂ق��ɉ�]�ƕ��q�Ԃ̐U��������̂ł����T�ɂȂ�܂��B
![]()
�C�̗��q�͂P���q�ɂ��čl����ƈʒu�x�N�g�����Ɖ^���ʃx�N�g�����ł���킹��
�ʑ���ԓ������v���ɑȉ~�^�����Ă���ƍl�����܂��B
�����A�m�̕��q���l����ƂQ�m�����̈ʑ���ԂɂP�_(��\�_)������
����ł��ׂĂ̕��q�̉^��������ł��܂��B
���̂悤�ȋ�Ԃ��u��(�K���})����v�Ƃ����܂��B
���ۂɂ́A���q�Ԃ̃G�l���M�[�̂��Ƃ肪�����Ȃ��炠��̂łP���q��
�ʑ���Ԃł̉^���͂��тȑȉ~�^���ɂȂ�܂��B
�����ŁA�S�̂̃G�l���M�[���d�`�d�{���d�̒��ɂ���Ƃ��܂��B
�i�A���A���d�͂d�Ɣ�ׂď\���������j
���̂悤�ȗ��q���u�������W�c�v�Ƃ����܂��B
![]()
�ʑ���Ԃ�����ȃZ���ŋ��ꍇ���l���܂��B
���̃Z���̖ʐς͂��������ŕ\���܂��B�������A���܂�ɂ��������Ƃ邱�Ƃ͂ł���
���� ��������
�łȂ���Ȃ�܂���B����́A�ʎq�͊w�̕s�m�萫���������邽�߂ł��B
�������Ăł����Z���ɓ����Ă��闱�q�̐�����1�C��2�C��3�C�E�E�E�Ƃ����
���q�������ꍇ�̐��v��
�v���@�@�@�@�@�m�I�@�@�@�@�@ �@�@��1�I ��2�I ��3�I�E�E�E
�ł��܂�܂��B���R�E�ł͗��q���Ƃ蓾��ꍇ�̐���傫�����悤�Ƃ���
����������܂��B�i������G���g���s�[�̑���̖@���Ƃ����܂��B�j
���ꂩ��A�G���g���s�[���킩����
�r����B�����v�@�@��B�F�{���c�}���萔�@�@�v�F�z�u��
���� �v!�łv�����ɑ傫���Ƃ��A���̂悤�ȋߎ����ł��܂��B
���� �v!���v(���� �v�|�P)
����́A�M���v�ł͔��ɗL���ł��B ������قǂ̔z�u���ɉ��p�����
�����v�������m!�|������ ��i!
�ɂȂ�܂��B�����v���ő�̂Ƃ��͂v���ő�ɂȂ�܂��B
![]()
�G�l���M�[�̕��ϒl�͎��̂悤�ɂ��ċ��߂邱�Ƃ��ł��܂��B
���������炅 exp(�|����)�������� �@�@�@�@��@ exp(�|����)�������� �@�@�@�� �R ���R��B�s�@�@���̎��͂P���q�̏ꍇ�ł��B �@�@�@�@�Q���@�@�Q
���̂悤�ɂ��ċ��܂�܂��B���q�̍��͑S�̂̃G�l���M�[�ɔ�Ⴕ�܂��B
����͋K�i���̂��߂ł��B
�P���R�x������̕��σG�l���M�[�����߂��
���������炅 exp(�|����)��������x �@�@�@�@��@ exp(�|����)��������x �@�@�@�� �P ����B�s �@�@�@�@�Q���@�@�Q
�ł��Ƃ܂�܂��B
![]()
�ʑ���Ԃł������̃Z��������܂��B
�����̊Ԃɂ̓G�l���M�[�̌���������̂ł����O������̃G�l���M�[�̂��Ƃ肪����܂���B
���̂悤�ȗ��q�̏W�c���u�����W�c�v�Ƃ����܂��B
����́A���q���m�A�̐ςu�A���x�s���w�肳�ꕽ�t�ɂȂ��Ă��܂��B
����́A�Z���ԂŃG�l���M�[�̌��������ł͂Ȃ����q�������\�Ȍn��
�l���܂��B������吳���W�c�Ƃ����܂��B
���w�|�e���V�����ʁA�̐ςu�A���x�s���w�肳�ꕽ�t�ɂȂ��Ă��܂��B
����́A�Z���Ԃ̃G�l���M�[�̌������S�G�l���M�[�Ɣ�ׂď\���������ꍇ�����肵�܂��B
������A�������W�c�Ƃ����܂��B
���q���m�A�̐ςu�A�G�l���M�[�d���w�肳�ꕽ�t�ɂȂ��Ă��܂��B
�ȏォ��w�肳���ϐ����ꗗ�ɂ��Ă݂܂����B
| �W�c�� | ���q�� | �̐� | �G�l���M�[ | ���x | ���w���ݼ�� |
| �����W�c | �m | �u | �@ | �s | �@ |
| �������W�c | �m | �u | �d | �@ | �@ |
| �叀�W�c | �@ | �u | �@ | �s | �� |