![]()
![]()
| 侾丆暘晍娭悢 | 俀崁丂億傾僢僜儞丂惓婯暘晍丂Bose-Fermi暘晍 |
| 俀丆棟憐僼僃儖儈婥懱 | Fermi暘晍娭悢丂Fermi僄僱儖僊乕丂Fermi攇悢 忬懺枾搙丂揹巕斾擬 |
| 俁丆棟憐儃乕僘婥懱 | Bose暘晍娭悢丂忬懺悢丂僨僶僀壏搙丂Bose嬅弅丂揮堏壏搙 |
暔棟偵偼寛掕榑揑側偙偲偲丄摑寁揑側傕偺偲偺俀偮偑偁傝傑偡丅
摑寁揑側傕偺偲偄偆偺偼丄暔棟尰徾傪妋棪揑側傕偺偲偟偰夝偔曽朄偱偡丅
擬摑寁椡妛偱偼丄偁傞偙偲偑婲偒傞妋棪(傑偨偼婜懸抣)偲偄偆偺偼
暘晍娭悢偱梌偊傜傟傑偡丅
偙偙偱丄崱傑偱妛廗偟偰偒偨暘晍娭悢傪傑偲傔偰傒傑偟偨丅
![]()
侾夞偺帋峴偱丄擟堄偺帠徾偑婲偒傞妋棪偑倫偩偲偟傑偡丅
偙偙偱倯傪擟堄偺帠徾偑婲偒側偄妋棪偲偡傞偲
倯亖侾亅倫
偵側傝傑偡丅俶夞偺帋峴偱擟堄偺帠徾偑値夞婲偙傞応崌偺悢偼
俛(n;N,p)亖N俠n丂倫n 倯N-n
偱梌偊傜傟傑偡丅偙偺偲偒丄暯嬒偼値倫丄暘嶶偼値倫倯偵側傝傑偡丅
![]()
億傾僢僜儞暘晍偼俀崁暘晍傪傕偭偲娙扨偵偟偨傕偺偱
俶佲侾丂丆丂倫佱侾
偵偍偄偰惉傝棫偪傑偡丅
偨偲偊偽曻幩慄曵夡偼丄曻幩慄尨巕偼旕忢偵懡偔(俶佲侾偵懳墳)
侾偮偺尨巕偵拝栚偟偨応崌侾昩偱曵夡偡傞妋棪偼傎偲傫偳侽偱偡丅(倫佱侾偵懳墳)
偙偺偲偒俀崁暘晍傪嬤帡偡傞偲
俹(n;兪)亖兪 exp(-兪) 丂丂丂丂丂丂丂値両
偨偩偟丄丂兪亖俶倫
偙偺偲偒丄暯嬒丄暘嶶丄偲傕偵兪偱偡丅
![]()
惓婯暘晍偼暿柤僈僂僗暘晍偲偄傢傟偰偄傑偡丅暯嬒兪丄暘嶶冃偺惓婯暘晍偼
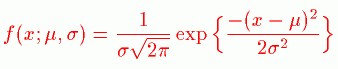
![]()
偙傟偼丄検巕椡妛揑側岠壥傪峫偊偨摑寁暘晍偱偡丅
俥倕倰倣倝暘晍娭悢偼師偺傛偆偵側傝傑偡丅

俛倧倱倕暘晍娭悢偼俥倕倰倣倝暘晍娭悢偵旕忢偵傛偔帡偰偄傑偡丅

徻嵶偵偮偄偰偼師偺復偱愢柧偟傑偡丅
擬丒摑寁椡妛侾偱偼屆揟揑側宯偵偮偄偰埖偭偰偒傑偟偨丅
偦偺偨傔丄棻巕摨巑偺憡屳嶌梡偼側偔丄検巕椡妛揑側岠壥偼峫偊傑偣傫偱偟偨丅
偟偐偟丄掅壏偵偍偄偰偼棻巕(摿偵揹巕)偼検巕揑側傆傞傑偄傪偟傑偡丅
偦偙偱丄擬丒摑寁椡妛俀偱偼検巕椡妛揑側岠壥偑偁傞宯偵偮偄偰峫偊傑偡丅
![]()
愭傎偳搊応偟偨僼僃儖儈暘晍娭悢偼師偺捠傝偱偡丅

偙傟偼丄棻巕偺懚嵼偡傞妋棫偺傛偆側傕偺偱偡丅
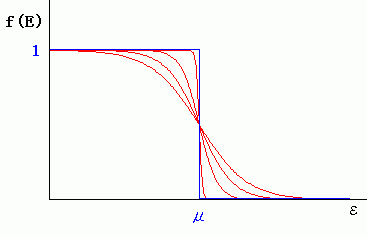
偨偲偊偽丄T亖侽偵偍偄偰偼兝仺亣偲側傝傑偡丅
偙偺偲偒丄兠亜兪側傜偽丄暘曣偼敪嶶偟丄倖亖侽偵側傝傑偡丅
媡偵兠亙兪側傜偽丄exp偺巜悢晹暘偼亅亣偵側傞偺偱 exp偼侽偵側傝傑偡丅偦偺寢壥丄倖亖侾乛侾亖侾偲側傝傑偡丅
偮傑傝丄俿亖侽偵偍偄偰偼兠亜兪偱偼倖亖侽丄兠亙兪偱偼倖亖侾 偲偄偆奒抜娭悢偵側傝傑偡丅(塃恾偺惵慄) 偙偺偲偒偺揹巕偼壜擻側尷傝僄僱儖僊乕偺掅偄忬懺偵偄傑偡丅
偙偙偐傜壏搙傪彊乆偵忋偘偰偄偔偲偩傫偩傫娚傗偐偵側偭偰偄偒傑偡丅
![]()
忋婰偺兪傪摿偵Fermi僄僱儖僊乕偲偄偄丄俤F偲偐偒傑偡丅
偙偺俤F偐傜師偺傛偆側傕偺偑媮傑傝傑偡丅
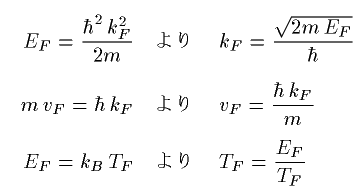
俲F傪Fermi攇悢丄倁F傪Fermi懍搙
俿F傪Fermi壏搙(弅戅壏搙)偲偄偄傑偡丅
![]()
偄傑偺暔棟検偺拞偱Fermi攇悢偼廳梫偱偡丅
攇悢倠偼T亖侽偵偍偄偰偼敿宎倠F偺媴撪偵偁傝傑偡丅
(偙偺媴柺傪乽Fermi柺乿偲偄偄傑偡丅)
傂偲偮偺攇偼(俀兾)3偺懱愊傪帩偮偲峫偊傑偡丅
傑偨丄揹巕偼俀偮偺揹巕忬懺偑偁傞偺偱場悢偺俀傪偮傑偡丅
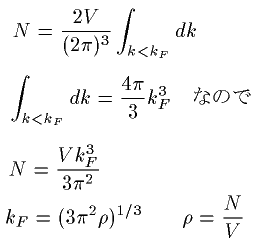
倁偼暔懱偺懱愊丄兿偼悢枾搙偱偡丅
偙傟偐傜俲F偑媮傔傜傟傑偡丅
栤戣 侾mol偺傾儖儈偺幙検偼27.0g丄枾搙偼2.69g/cm3偱偡丅 偙偺偲偒偺Fermi攇悢傪媮傔傛丅 夝摎 丂懱愊倁偼丄27.0/2.69=10.0cm3=1.00亊10-5m3 侾偮偺傾儖儈尨巕偵偼俁偮偺揹巕偑懚嵼偡傞偺偱 悢枾搙兿偼丄兿亖俶亖3亊6.02亊1023亖1.81亊1029[m-3] 丂丂丂丂丂丂丂丂倁丂 1.00亊10-5 倠F亖(俁兾2兿)亖1.75亊1010 [m-1] 傑偨丄 倴T亖2.03亊106 [m/s] 俿T亖1.35亊105 [K] 俤T亖1.87亊10-18 [J]亖11.6 [eV]
偙偺傛偆偵Fermi壏搙偼偐側傝崅壏側偺偱丄忢壏偱偼嬥懏撪偺揹巕偼
Fermi婥懱偺傛偆偵怳晳偄傑偡丅偙偺傛偆偵Fermi壏搙偲斾傋偰
廫暘偵掅壏側応崌偼Fermi摑寁偑棙偄偰偒傑偡丅
![]()
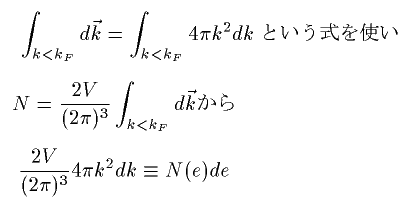
偙偺傛偆偵偟偰忬懺枾搙俶(e)傪掕媊偟傑偡丅(棻巕悢N偲偼娭學偁傝傑偣傫丅)
嵍曈偼丄倠乣倠亄dk偵偍偄偰偺壜擻側侾棻巕忬懺偺悢偱丄
塃曈偼丄倕乣倕亄de偱偺忬懺悢傪昞偟傑偡丅
偙偺忬懺枾搙偼僄僱儖僊乕倕偺暯曽崻偵斾椺偟傑偡丅
![]()
嬥懏偺掅壏偱偺斾擬偺怳傞晳偄傪娤應偡傞偲師偺傛偆偵側傝傑偡丅
俠v亖兞俿亄俙俿3
塃曈戞1崁偼俿偵斾椺偟偰偄傑偡丅偙傟偼検巕椡妛揑側岠壥偑
尰傟偨傕偺偱丄乽揹巕斾擬乿偲偄偄傑偡丅
戞2崁偼俿3偵斾椺偟偰偄傑偡丅偙傟偼奿巕怳摦偵傛傞傕偺偱偡丅
暔幙撪偱偼丄桳尷偺壏搙偑梌偊傜傟偰偄傞偨傔奿巕怳摦偲偄偆傕偺偑偍偒傑偡丅
偙傟傪僼僅僲儞(壒巕)偲偄偆堦庬偺棻巕偲偟偰娫偑傞曽朄偼
暔惈暔棟妛侾偱徯夘偟傑偟偨丅
偙偺僼僅僲儞偼丄Bose棻巕偺傛偆側怳傞晳偄傪偟傑偡丅
Bose棻巕偲偼丄1偮偺棻巕忬懺偵偄偔偮傕偺棻巕偑擖傟傞傛偆側棻巕偺偙偲偱偡丅
(Fermi棻巕偼俀偮傑偱偱偡丅)
Bose棻巕偺椺偲偟偰丄僿儕僂儉尨巕妀丄僼僅僩儞丄僼僅僲儞側偳偑偁傝傑偡丅
![]()
愭傎偳搊応偟偨Bose暘晍娭悢偼師偺捠傝偱偡丅

偙偺偲偒丄壔妛揑億僥儞僔儍儖兪偼侽偐晧偱偁傞昁梫偑偁傝傑偡丅
(兪亜侽偩偲丄兠亙兪偺偲偒丄倖亙侽偵側偭偰偟傑偆丅)
![]()
僼僅僲儞偵偮偄偰丄攇悢傪倯偱昞偟傑偡丅(愭傎偳偺k偲嬫暿偟傑偡丅)
偝傜偵丄暔幙撪傪揱傢傞廲攇偺懍搙傪倱l丄墶攇傪倱t偲偟傑偡丅
倯乣倯亄倓倯撪偵偁傞挷榓怳摦巕偺悢偼師偺傛偆偵寁嶼偱偒傑偡丅
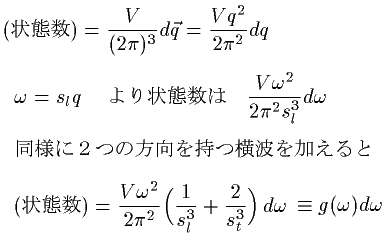
偙偺g(冎)偼冎乣冎亄倓冎偵偁傞挷榓怳摦巕偺悢傪昞偟傑偡丅
(忬懺枾搙N(e)偲堘偆偺偱拲堄偟偰偔偩偝偄丅)
g(冎)偼冎偺俀忔偵斾椺偟傑偡丅
偟偐偟丄暔幙偼楢懕懱偱偼側偔丄尨巕偱偱偒偰偄傞偨傔冎偵傕忋尷偑偁傝傑偡丅
偦傟傪冎D偲偡傞偲倗(冎)娭悢偼丄侽乣冎D傑偱偑冎2偵斾椺偟偰
冎D埲忋偱偼侽偵側傝傑偡丅
偙偺傛偆側奿巕怳摦偵懳偡傞柾宆傪僨僶僀柾宆偲偄偄傑偡丅
冎D傪梌偊傞倯D偼師偺傛偆偵偟偰傕偲傑傝傑偡丅
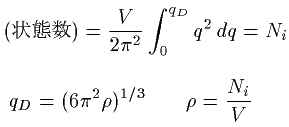
![]()
![]()
偱偁傜傢偝傟偨儲傪僨僶僀壏搙偲偄偄傑偡丅
僨僶僀壏搙偼戝懱悢昐[K]偺僆乕僟乕偱偡丅
偙傟偐傜僄僱儖僊乕倀偑師偺傛偆偵嬤帡偱偒傑偡丅
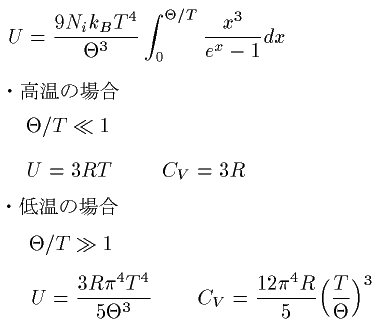
側偍丄CV偼師偺傛偆偵偟偰傕媮傑傝傑偡丅
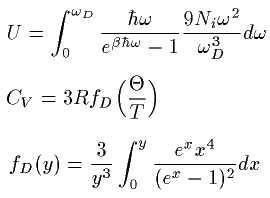
偨偩偟丄俼亖俶i倠B
偙偺倖D傪僨僶僀娭悢偲偄偄傑偡丅
偙傟偼丄倷仺侽偱倖D仺侾偵側傝丄屆揟摑寁椡妛偵懳墳偟傑偡丅
![]()
愨懳侽搙偺偲偒丄Bose棻巕偼倠偺侾棻巕忬懺偵偄偔傜偱傕擖傞偙偲偑偱偒傞偺偱
倠亖侽偺忬懺偵偡傋偰偺棻巕傪廂梕偡傟偽偄偄偙偲偵側傝傑偡丅
偙偺傛偆偵丄侾棻巕忬懺偵嫄帇揑側悢偺Bose棻巕偑嬅弅偡傞尰徾傪
Bose嬅弅偲偄偄丄嬅弅偟偰偄傞棻巕傪嬅弅懱偲偄偄傑偡丅
![]()

(6)偺偙偲傪乽儕乕儅儞偺兡娭悢乿偲偄偄傑偡丅
兛亖侽偼掅壏偺忬懺偱幚尰偟傑偡丅
![]()
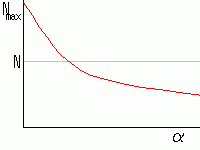 忋偺(俆)幃偺塃曈戞2崁偲兛偺娭學偼塃恾偺傛偆偵側傝傑偡丅
忋偺(俆)幃偺塃曈戞2崁偲兛偺娭學偼塃恾偺傛偆偵側傝傑偡丅
Bose嬅弅偑婲偒傞偲偒偼丄値0亜侽丄兛亖侽側偺偱
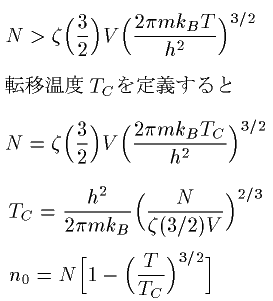
偙偺俿俠偑乽揮堏壏搙乿偲偄偆傕偺偱偡丅俿亙俿俠偩偲丄Bose嬅弅偑婲偒傑偡丅
Bose嬅弅傪婲偙偟偨棻巕偺悢偼丄俿亖俿俠偱侽丄俿亖侽偱俶偲側傝傑偡丅
偙偺揮堏壏搙俿俠偺慜屻偺暔幙偺惈幙偼晄楢懕偵側傝傑偡丅
(偮傑傝丄惈幙偑曄傢偭偰偟傑偄傑偡丅)
栤戣 1mol偺塼懱僿儕僂儉偼27.6cm3偺懱愊傪偟傔傑偡丅 偙偺偲偒丄塼懱僿儕僂儉偺揮堏壏搙傪媮傔傛 夝摎 He尨巕偺幙検偼 倣亖丂丂係丂丂丂亖丂6.64亊10-27 [kg] 丂丂6.02亊1023 兡(3/2)亖2.612 兿亖俶亖6.02亊1023亖2.18亊1028 [m-3] 丂丂倁丂27.6亊10-6 偙傟傜傪愭傎偳偺俿c傪媮傔傞幃偵戙擖偡傞偲 俿c亖3.14[K]