![]()
![]()
| 1,回折 | ブラッグの散乱 逆格子ベクトル 回折 ミラー指数 ブリルアンゾーン |
| 2,原子の運動 | 原子の運動 運動方程式 散乱 フォノン分光 |
コヒーレントな光を結晶に当てた場合
2d sinθ=nλ
という条件を満たしたとき、結晶から強く反射します。
これを「ブラッグ散乱」といいます。
![]()
rを結晶の位置ベクトルとすると
exp(r・G)=1
を満たすようなGを「逆格子ベクトル」といいます。
この条件は、次のように書き換えることも可能です。
G・rn=2πm
また、rn=n1a1+n2a2+n3a3 gn=hg1+kg2+lg3とすると、
gi・aj=2πδij
となります。ajとgiの関係は次のようになります。
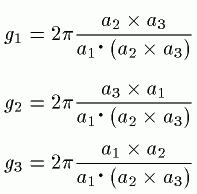
つまり、逆格子Gのi成分は、位置ベクトルrのj,k成分のなす平面に
垂直に交わります。(i≠j≠k)
キッテルの本には次のようなことが載っています。
「結晶の回折パターンは、その結晶の逆格子の地図であり、
顕微鏡像は、現実の空間における結晶構造の地図である。」
これからもわかるように、回折像を考察する際には逆格子ベクトルの
考え方が重要になります。
逆格子ベクトルの次元は[m-1]という次元になります。
![]()
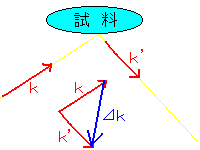
図のように試料に波動ベクトルkを入射させ、k’の反射があった場合を
考えます。このとき、波動ベクトルkの変化量⊿kは
⊿k=k’-kで決まり、図の下のようになります。
このとき、⊿kと試料の逆格子ベクトルGは次のような関係があります。
⊿k=G
これをラウエ条件といいます。
![]()
1直線状にない3個の格子点は平面を作ります。
この平面に次のようにしてラベル付けをすることができます。
まず、この平面と座標軸との交点がそれぞれm,n,oで交わったとしましょう。
このm,n,oは基底ベクトルを単位としてその整数倍になっています。
これらの逆数をh=1/m,k=1/n,l=1/oにします。
さらに、このh,k,lを整数p倍して互いに素な整数組(h,k,l)を作ります。
h,k,lを格子面(h,k,l)のミラー指数といいます。
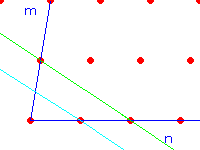
たとえば、m=1,n=2,o=2のとき、上図の緑色の平面になります。
(ただし,m,nについてのみでoは図に載っていません。)
逆数は、h=1,k=1/2,l=1/2です。
これをp=2倍することでh=2,k=1,l=1という互いに素な整数組になります。
これから、この面のミラー指数は(2,1,1)になります。
これに平行な面m=2,n=4,o=4の場合でもp=4になり、
ミラー指数は(2,1,1)になります。ところで、p=2の場合ですが
実は、この平面と原点の間には別の面が存在します。
これが、図の水色で示した平面です。
p=4の場合では、自身を含め原点の間に4つの平面があります。
![]()
ブラッグ反射の起こる条件は⊿k=Gです。このような条件を満たす
k、k’のベクトルの始点はGの垂直2等分線上にあります。(回折の項目参照)
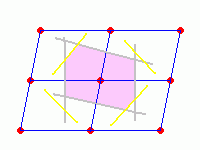
図の場合、逆格子面の垂直2等分線を灰色、黄色の順で書いてあります。
これより、第1ブリルアンゾーンは図のピンク色の部分になります。
固体の物理的性質は主に次の2つで決まります。
前者の性質は、化学変化、光、結合などに関係しています。
後者は熱、物体に硬さなどに関係してきます。
特に物体の硬さは構造欠陥が決定的な役割を果たします。
ここで、結晶の全エネルギーをΦとします。
原子核が平衡点にあるときはΦ(rnαi)で表されます。
そこから微少(snαi)だけずらしたときのエネルギーはTaylor展開すると
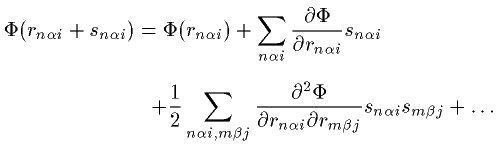
この展開はエネルギーが平行な状態のあたりで展開されているので
リニアな項は消滅します。そのため右辺第2項は消えます。
すると、今の式は調和振動子のポテンシャルを多粒子系に拡張したものになっています。
また、2階偏微分の部分はばね係数「k」と同じ次元を持ちます。
この部分は、次のようにおくことにします。
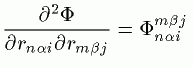
このΦを「結合定数」といいます。
結合定数は空間の等方性、並進不変性、点郡対称性という条件を
満たすように決められます。
![]()
ニュートンの法則によって次のような条件があります。
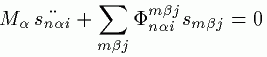
ここで、snαiを単位胞の座標の平面波で表せます。
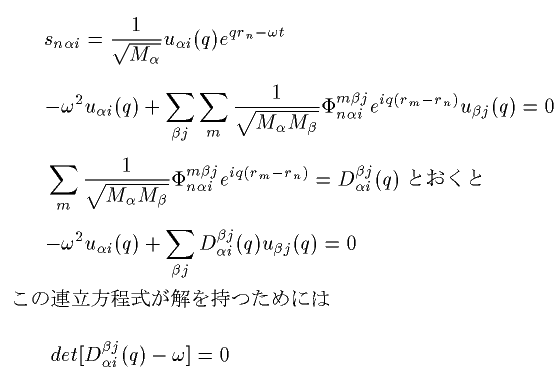
具体的な例として2原子1次元鎖について今のdetをあてはめると
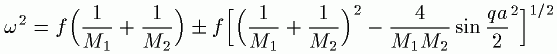
これから、qの周期が2π/aで、逆格子ベクトルに等しくなっています。
これから、次のようなことがいえます。
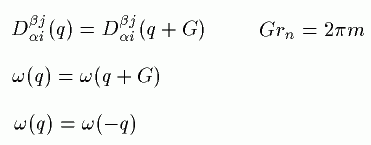
![]()
原子に対する運動方程式の解は、平面波の形を持ちます。
単純格子においては、散乱振幅は次のような形を持ちます。
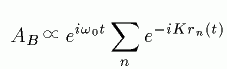
ここで、時間に依存するrnを分離することで次のようになります。

最後に2つの式が出てきましたが、前半がエネルギー保存則といいます。
後半は、hqを波である結晶振動の準運動量と仮定すれば
準運動量の保存則と解釈できます。
これから、今のような波を粒子をみなすことができます。
これをフォノン(音響粒子)とみなすことができます。
また、ωo、koは、結晶に入射する前の波の状態で、ω、kは入射後の状態です。
入射の前後では、hq、hω(q)だけ変化しています。
これは、結晶内のフォノンとの相互作用で、まるで粒子との衝突のように見えます。
![]()
可視光線およびその近傍の光の非弾性散乱はラマン散乱
音波との相互作用はブリルアン散乱といいます。
可視光線の散乱による波数の変化は逆格子ベクトルの1/1000程度
しかないので、ラマン散乱はq=0付近での格子振動の観察が中心です。
しかし、X線では光子エネルギーが104eVあるのに対し
フォノンは10-3eV程度しかなく、観測には107程度の
精度が必要で、実際には困難です。
それに対し、中性子や原子線では0.1~1eVしかなく、
精度が103程度で済むので、現在はこちらの観測が主流です。