![]()
![]()
| 1,惑星の方程式 | |
| 2,ケプラーの法則 | 第1法則 第2法則 第3法則 |
| 3,スィングバイ | スィングバイなし スィングバイあり スィングバイの効果 |
人工衛星、ボイジャー1号,2号、パイオニア、最近ではカッシーニなど
惑星探査においてたびたび「スィングバイ」という言葉が登場しました。
スィングバイとは、惑星の重力を使って衛星を加速する方法です。
スィングバイのレポートがあります。文章はWord98形式になっています。
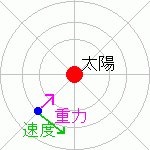
太陽系の惑星の運動を考えるとき、中心に太陽を固定し
その周りを惑星が回っていると考えます。
座標は極座標表示にして、原点を太陽にします。
こう考えると、惑星に働く力は太陽による重力のみとなります。
(この力を中心力といいます。
このような考え方は電磁気、原子にも応用できます。)
すると惑星の運動方程式は、r軸方向とθ軸方向に分離できます。
しかも、θ軸方向には力はありません。
これらをふまえて惑星の運動方程式を作ります。
Fr = mAr −−−−−(1) Fθ = mAθ −−−−−(2)
ここで、Frはr方向の力、Arはr方向の加速度と考えます。
極座標では、r,θ方向の速度、加速度は次のようになります。
Vr = dr dt Vθ = r dθ dt Ar = d2r −r d2θ dt2 dt2 Aθ = 2 dr dθ + r d2θ = 1 d (r2θ') dt dt dt2 r dt
※r'はrの一階時間微分 r"はrの二階時間微分を表しています。
また、力は、r方向の重力のみなので
Fr = −GMm r2 Fθ = 0
これを、(1),(2)に代入すると
m(r" − rθ'2) = −GMm −−−−−(3) r2 m d (r2θ') =0 −−−−−(4) r dt
これを簡単にすると次のようになります。
r" − rθ'2 + GM = 0 −−−−−(5) r2 d(r2θ') = 0 −−−−−(6) dt
これが惑星の運動方程式です。
(これは、電荷、古典的な原子論でも用いることができます。)
「惑星は太陽を1つの焦点とする楕円軌道を描く」
というものがケプラーの第1法則です。では、実際に導いてみましょう。
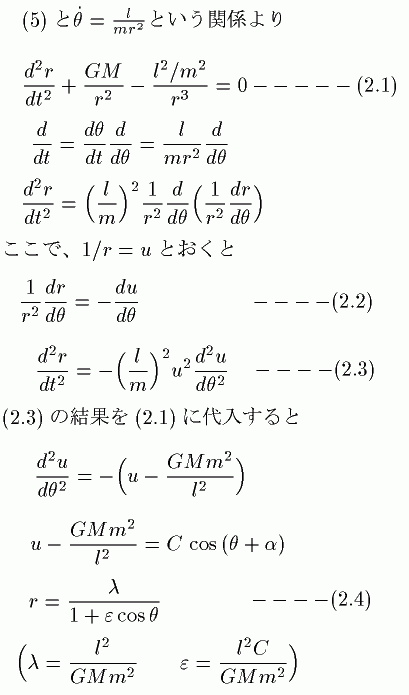
この(2.4)式が惑星の方程式です。
εの値によって次のような軌道になります。
0<ε<1 ・・・・楕円 ε= ・・・・放物線 ε>1 ・・・・双曲線
![]()
「惑星と太陽を結ぶ線分が一定時間に描く扇形の面積は常に一定である」
というものがケプラーの第2法則です。これは、簡単に証明できます。
前章の(6)式をご覧ください。時間微分したものが0ということは、
r2θ' = 一定
ということです。実は、これが単位時間あたりに描く扇形の面積になっています。
このように簡単に証明できます。
![]()
「惑星の公転周期の2乗と、長半径の3乗の比はすべての惑星で共通である」
というものがケプラーの第3法則です。これも導いてみます。

これより、周期Tの2乗と長径の3乗の比は惑星によらず一定になります。
ここでは、具体的な例として、地球から出発したロケットが
天王星に向かう場合を考えます。
![]()
まず、スィングバイをしないで天王星に直接向かう場合を考えます。
衛星は地球を近日点、天王星を遠日点とする楕円軌道を描きます。
近日点での太陽からの距離は1AU、遠日点では19.2AUです。
これから、下の式を使ってε=0.9,λ=1.0がもとまります。
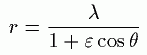
さらに、長径と短径が「ケプラーの第3法則」で使った式から
a=10.1AU、b=4.4AUともとまります。
さらにケプラーの第3法則から、周期が32年なので
地球→天王星までは16年かかります。
また地球を出発するときに必要な速度は、41km/sです。
ただし、地球は元々太陽も周りを30km/sで公転しているので
地球の公転方向に11km/sだけ加速すればいいことになります。
![]()
では、木星でスィングバイを行ってから天王星に向かう場合を考えてみます。
この場合のスィングバイは3段階あります。
| 行 程 | 基準系 |
| 地球から木星まで | 太陽 |
| ↓ | |
| 木星でのスィングバイ | 木星 |
| ↓ | |
| 木星から天王星まで | 太陽 |
地球から木星までは楕円軌道になります。
この楕円軌道は先程の天王星まで行くための楕円軌道と同一ものもにします。
エネルギー保存則より木星到達時の速度が16km/sと求まります。また、
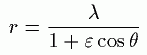
からθ=135度が求まります。また、所要時間は角運動量Lから
所要時間がθで積分する事で求まり、1.25年と求まります。
ここでは、太陽だけではなく、木星による影響も大きく関係します。
そこで、太陽を基準とした座標系と、木星を中心とした座標系を導入します。
| 変数 | 基準系 | 意味 |
| pi | 太陽 | 木星接近直前のロケットの運動量 |
| pf | 太陽 | 〃 直後の 〃 |
| pi' | 木星 | 〃 直前の 〃 |
| pf' | 木星 | 〃 直後の 〃 |
また、木星自体の速度をVJとします。運動量については次のガリレイ変換を満たします。
pi'=pi−mVJ pf'=pf−mVJ
運動量の変化量は
Δp=pf−pi
=pf'−pi'
=Δp'
これから各座標系で等しいことがわかります。これに対してエネルギーは
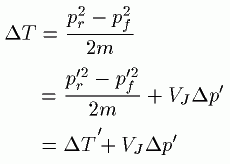
このように、座標系によってエネルギーの変化量が変わります。
ところで、ΔT'は木星を固定した場合の運動エネルギーの変化量ですが、
接近前の速度と接近後の速度は、木星の質量が衛星と比べて遙かに大きいので
変化しないと考えられます。このためΔT'=0になります。
スィングバイによって、ΔT=VJ・Δpだけエネルギーを得するわけです。
このときの軌道は、双曲線になります。
次に、速度について考えてみます。
| 変数 | 基準系 | 意味 |
| vi | 太陽 | 木星接近直前のロケットの速度 |
| vf | 太陽 | 〃 直後の 〃 |
| ui | 木星 | 〃 直前の 〃 |
| uf | 木星 | 〃 直後の 〃 |
ガリレイ変換から次の式ができます。
ui=vi−VJ uf=vf−VJ
また、uiとujの大きさは等しいので
|ui|=|uf|=u
とおけます。vi=16km/s,VJ=13km/sがわかっているので
u=14.7km/s がもとまります。
さて、スィングバイによってロケットが最大のエネルギーをもためには
VJとvfが平行なときであることは上の式から自明です。
では、幾何学的に解いてみます。
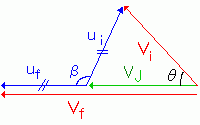 |
viが太陽座標での接近前の速度、vfが接近後の速度です。 これから、vf>viがわかります。 また、ufとuiの大きさが同一であることもわかります。 |
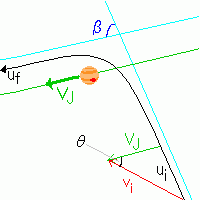 |
木星を固定した系で見ると左のようになっています。 太陽を固定した系では、ロケットは θ度だけ曲げられていることがわかります。 |
βは計算でき、β=109度がわかります。速度については
vf=uf+VJ =13+14.7=27.7km/s
ということがわかります。これで、木星でのスィングバイによって
16km/sから27.7km/sに加速されたことがわかりました。
木星から天王星までの軌道は、
E=1mvf2 − GMm 2 rJ =3.8×108−1.7×108[J]>0
なので、双曲線になります。では、この双曲線の式を求めてみましょう。

これに天王星の軌道r=19.2[AU]を代入することで
θ=86.7度が求まります。
また、角運動量の式から
所要時間がθで積分する事で求まり、3.4年とわかります。
![]()
以上の結果から、地球から出発するときの初速度は同じであるにもかかわらず
スィングバイを利用しなかった場合は16年かかったものが
スィングバイを木星で行うことで1.3+3.4=4.7年ですむことになります。
このことからスィングバイの効果は絶大であることがわかります。
人工衛星がエネルギーを得たということは、木星がエネルギーを失ったということになります。
仮に探査衛星の質量を100kgとすると、エネルギー保存則より
ΔE=1m(Vf−Vi) =100×(27.72−162)/2 2 =2.55×104[J]
つまりこれだけのエネルギーの授受があったことになります。
dE=GMm dr 2r2
からdrが1.22×10-19[m]ということがわかり
ほとんど木星は落下しないことがわかります。
また、木星の公転速度は1.03×10-27[m/s]だけ速くなります。
(運動エネルギーは大きくなりますが、それ以上に位置エネルギーが減少します。)
 今までは、スィングバイを用いて加速することを
今までは、スィングバイを用いて加速することを
考えていましたが探査を終えたロケットが
地球に帰還することもあります。
そのときは、今の曲線の反対方向にロケットを進めれば
いいような気がしますが惑星は常に同じ方向に動いているので
そうはいきません。
減速するには惑星との相対速度が小さくなるように、なるべく
軌道の接線方向から近づけばいいわけです。