![]()
![]()
| 侾丆俀師娭悢 | 俀師娭悢偺僌儔僼丂嵟戝抣丒嵟彫抣丂敾暿幃 |
| 俀丆嶰妏斾 | 扨埵墌丂嶰妏斾偺岞幃侾丂嶰妏斾偺岞幃俀丂惓尫掕棟丂梋尫掕棟丂嶰妏宍偺柺愊 |
| 俁丆妋棪 | 奒忔丂弴楍丂慻傒崌傢偣 |
崅峑悢妛偼栚埨偲偟偰埲壓偺傛偆偵妛廗偟偰偄偒傑偡丅
| 妛擭 | 暘栰 | 撪梕 |
| 侾 | 悢侾 | 俀師娭悢丂嶰妏斾丂屄乆偺張棟丂妋棪 |
| 悢俙 | 悢偲幃丂悢楍丂暯柺婔壗 | |
| 俀 | 悢俀 | 恾宍偲幃丂嶰妏娭悢丂巜悢偲懳悢丂旝暘丂愊暘 |
| 悢俛 | 暋慺悢丂儀僋僩儖丂妋棪暘晍 | |
| 俁 | 悢俁,俠丂 | 旝暘丂愊暘 |
乽倷偼倶偺娭悢偱偁傞乿
偙傟偼倶偺抣傪寛傔傞偲帺摦揑偵倷偺抣傕寛傑偭偰偟傑偆偲偄偆偙偲偱偡丅
悢妛揑偵偼倷亖倖(倶)偲昞偟傑偡丅
倶偺偲傝偆傞斖埻傪掕媊堟丄 倖(倶)偺偲傝偆傞斖埻傪抣堟偲偄偄傑偡丅
俀師娭悢偼堦斒揑偵
倷亖倎倶2亄倐倶亄們
偁傞偄偼
倷亖倎(倶亅倫)2亄倯
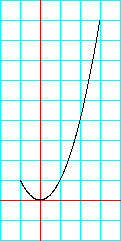
偱昞偣丄倶2偺學悢偑惓(倎亜侽)偺偲偒丄僌儔僼偼忋偵
奐偒傑偡丅倎亙侽偺偲偒偼壓偵奐偒丄倎亖侽偩偲捈慄偵側傝傑偡丅
傑偨丄乥倎乥偑戝偒偄偲俀師娭悢偺奐偒曽偑嫹偔側傝傑偡丅
倷亖倎倶2
傪婎杮偺俀師娭悢偲偟偨偲偒
倷亖倎(倶亅倫)2亄倯
偼婎杮偺俀師娭悢傪倶幉曽岦偵倫丄倷幉曽岦偵倯偩偗堏摦偟偨娭悢偱偡丅
栤戣侾 俁揰(亅侾丆侽),(侽丆俆),(俁丆亅係)傪捠傞俀師娭悢傪媮傔傛 夝摎侾 俀師娭悢偺堦斒偺宍偼 倷亖倎倶2亄倐倶亄們 偱昞偣傑偡丅偙傟偵戙擖偟偰楢棫曽掱幃傪偨偰傟偽偄偄傢偗偱偡丅 丂乛丂侽亖倎亅倐亄們 乥 丂俆亖們 丂乢亅係亖俋倎亄俁倐亄們 倎亖亅俀丂倐亖俁丂們亖俆 倷亖亅俀倶2亄俁倶亄俆 栤戣俀 捀揰偺嵗昗偑乮侾丆俀乯偱乮亅侾丆俇乯傪捠傞俀師娭悢傪媮傔傛 夝摎俀 俀師娭悢偼堦斒偵 倷亖倎(倶亅倫)2亄倯 偱昞偣傑偡丅嵗昗偑乮侾丆俀乯側偺偱 倫亖侾丂倯亖俀 偝傜偵乮亅侾丆俇乯傪捠傞偺偱 俇亖倎(亅侾亅侾)2亄俀 倎亖侾 傛偭偰 倷亖(倶亅侾)2亄俀
![]()
 倶偺掕媊堟偑丂倎亙倶亙倐丂偱昞偣傞傕偺偲偟傑偡丅
倶偺掕媊堟偑丂倎亙倶亙倐丂偱昞偣傞傕偺偲偟傑偡丅
傕偟丄倷亖倖(倶)丂偑侾師娭悢偺偲偒偼倷偺抣堟偼
倖(倎)亙倷亙倖(倐)丂偐偦偺媡偵側傝傑偡丅丂
偟偐偟丄俀師娭悢偺偲偒偼堘偭偰偒傑偡丅
椺偲偟偰倶偺掕媊堟偑丂亅侾亙倶亙俁偱倷亖倶2
偱昞偣傞娭悢偼塃恾偺傛偆偵側傝傑偡丅
偙傟傛傝侾亙倷亙俋偱偼側偔丄侽亙倷亙俋偱偁傞偙偲偑傢偐傝傑偡丅
俀師娭悢偱偼掕媊堟偺椉抂埲奜偵捀揰傕峫椂偡傞昁梫偑偁傝傑偡丅
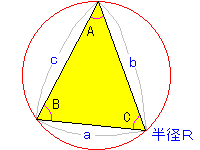
![]()
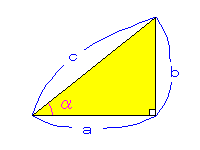
俀師娭悢偑倶幉偲偺岎揰傪帩偮偐敾暿偱偒傞幃偑偁傝傑偡丅
偙傟偼丄敾暿幃偲偄偆傕偺偱棯偟偰俢偲彂偒傑偡丅
俀師娭悢傪
倷亖倎倶2亄倐倶亄們
偲偍偄偨偲偒敾暿幃偼師偺傛偆偵側傝傑偡丅
俢亖倐2亅係倎們
偙偺偲偒偺俢偺抣偵傛偭偰娭悢偲倶幉偲偺娭學偑傢偐傝傑偡丅
俢亜侽丂丂丂堎側傞俀揰偱岎傢傞 俢亖侽丂丂丂侾揰偱愙偡傞 俢亙侽丂丂丂岎傢傜側偄
栤戣侾 倶幉偲倷亖倶2亅俀倶亅侾偺娭學傪偺傋傛 夝摎侾 俢亖(亅俀)2亅係丒侾丒(亅侾) 丂亖俉亜侽 傛偭偰堎側傞俀揰偱岎傢傞 栤戣俀 倷亖倶2亅俀倶亄倠丂偑倶幉偲堎側傞俀揰偱岎傢傞傛偆側 斖埻傪媮傔傛 夝摎俀 俢亖(亅俀)2亅係丒侾丒倠亜侽 倠亙侾 栤戣俁 倷亖倶2亅係倶亄俆丂偲丂倷亖倶亄侾偺 嫟桳揰偺屄悢偲偦偺嵗昗傪媮傔傛 夝摎俁 倶2亅係倶亄俆亖倶亄侾 倶2亅俆倶亄係亖侽亅亅亅亅亅亅亅亅亅亅嘆 俢亖(亅俆)2亅係丒侾丒係 丂亖俋亜侽 傛偭偰堎側傞俀揰偱岎傢傞丅 嘆傛傝丄倶亖侾丆係丂偦偺偲偒偺倷偺抣偼倷亖俀丆俆 傛偭偰乮侾丆俀乯丆乮係丆俆乯
 嶰妏斾偼捈妏嶰妏宍偺偁傞妏搙(捈妏偱偼側偄晹暘)偺妏偑
嶰妏斾偼捈妏嶰妏宍偺偁傞妏搙(捈妏偱偼側偄晹暘)偺妏偑
梌偊傜傟偰偄傞偲偒偺奺曈偺挿偝偺斾偺偙偲偱偡丅
偙傟偵偼丄俁庬椶偁偭偰偦傟偧傟倱倝値丆們倧倱丆倲倎値偱昞偟傑偡丅
塃恾偺傛偆側嶰妏宍偑偁傞偲偒嶰妏斾偼師偺傛偆偵昞偣傑偡丅
倱倝値兛亖倐乛們 們倧倱兛亖倎乛們 倲倎値兛亖倐乛倎
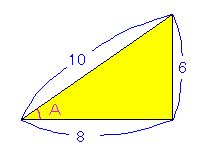
栤戣 塃恾偺傛偆側嶰妏宍偑偁傞偲偒 倱倝値俙丆們倧倱俙丆倲倎値俙傪傕偲傔傛 夝摎 倱倝値俙亖俇乛侾侽亖俁乛俆 們倧倱俙亖俉乛侾侽亖係乛俆 倲倎値俙亖俇乛俉丂亖俁乛係
倱倝値丆們倧倱丆倲倎値抣偼師偺傛偆偵寛傑偭偰偄傑偡丅
| 妏搙 | 侽 | 俁侽 | 係俆 | 俇侽 | 俋侽 |
| 倱倝値 | 侽 | 侾乛俀 | 侾乛併俀 | 併俁乛俀 | 侾 |
| 們倧倱 | 侾 | 併俁乛俀 | 侾乛併俀 | 侾乛俀 | 侽 |
| 倲倎値 | 侽 | 侾乛併俁 | 侾 | 併俁 | 亅 |
嶰妏斾偼侽乣俋侽搙傑偱偼埫婰偡傞昁梫偑偁傝傑偡丅
偟偐偟丄偦傟埲忋偼埲壓偺岞幃傪巊偭偰媮傔傞偙偲偑偱偒傑偡丅
![]()
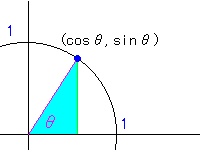 嶰妏斾偼扨埵墌傪巊偭偰峫偊傞偲傢偐傝傗偡偔側傝傑偡丅
嶰妏斾偼扨埵墌傪巊偭偰峫偊傞偲傢偐傝傗偡偔側傝傑偡丅
扨埵墌偼敿宎偑侾偺墌偱尨揰偵拞怱傪帩偭偰偒傑偡丅
偙偺墌忋偵揰傪懪偪丄倶幉偲側偡妏傪兤偲偟傑偡丅
偡傞偲丄倶嵗昗偼們倧倱兤丄倷嵗昗偼倱倝値兤偵側偭偰偄傑偡丅
偙偙偵倶亖侾偲偄偆捈慄傪堷偄偰傒傑偡丅
尨揰偐傜揰傪捠傞捈慄傪偺偽偟偰倶亖侾傪岎傢傝傑偡丅
偙偺偲偒偺倷嵗昗偺抣偑倲倎値兤偺抣偱偡丅
揰偼扨埵墌忋偟偐堏摦偱偒側偄偺偱們倧倱兤丄倱倝値兤偺偲傝偆傞斖埻偼
師偺傛偆偵寛傑偭偰偟傑偄傑偡丅
亅侾亝們倧倱兤亝侾 亅侾亝倱倝値兤亝侾
倲倎値兤偺抣偼帺桼偵偲傟傑偡丅
![]()
嶰妏斾偺妏搙偼侾廃偟偰偟傑偆偲尦偺忬懺偵栠偭偰偟傑偄傑偡丅
偙傟偼丄扨埵墌偱峫偊傞偲傢偐傝傗偡偄偲巚偄傑偡丅
倱倝値(俁俇侽亄兤)亖倱倝値兤 們倧倱(俁俇侽亄兤)亖們倧倱兤 倲倎値(俁俇侽亄兤)亖倲倎値兤
偱偼丄兤偵侾俉侽搙偨偟偨応崌傪峫偊傑偡丅
偙偺偲偒丄扨埵墌偺嶰妏宍偼戞侾徾尷偐傜戞俁徾尷偵堏摦偡傞偺偱
倶嵗昗偺們倧倱兤丄倷嵗昗偺倱倝値兤偺抣偑斀揮偟傑偡丅
偟偐偟丄倲倎値兤偼曽岦偑曄傢傞偩偗偱尦偺捈慄偲暯峴偱偡丅
倱倝値(侾俉侽亄兤)亖亅倱倝値兤 們倧倱(侾俉侽亄兤)亖亅們倧倱兤 倲倎値(侾俉侽亄兤)亖倲倎値兤
侾俉侽搙偐傜兤傪堷偄偨応崌偼扨埵墌偺嶰妏宍偑
倷幉傪懳徾偲偡傞埵抲偵堏摦偟偰偄傑偡丅
廬偭偰丄倶偺晞崋偼斀揮偟丄倷偼晄曄丄倲倎値偺晞崋偼斀揮偟傑偡丅
倱倝値(侾俉侽亅兤)亖倱倝値兤 們倧倱(侾俉侽亅兤)亖亅們倧倱兤 倲倎値(侾俉侽亅兤)亖亅倲倎値兤
偙偺偲偒偼倶偲倷偺棫応偑擖傟懼傢偭偰偄傞偺偱師偺傛偆偵側傝傑偡丅
倱倝値(俋侽亅兤)亖倱倝値兤 們倧倱(俋侽亅兤)亖們倧倱兤 倲倎値(俋侽亅兤)亖侾乛倲倎値兤
偙偺偲偒偼倶仺倷丄倷仺亅倶偲偄偆曄姺偑偍偒偰偄傑偡丅
倱倝値(俋侽亄兤)亖們倧倱兤 們倧倱(俋侽亄兤)亖亅倱倝値兤 倲倎値(俋侽亄兤)亖亅侾乛倲倎値兤
![]()
倱倝値丆們倧倱丆倲倎値偺娫偵傕岞幃偑偁傝傑偡丅
倱倝値2兤亄們倧倱2兤亖侾 倲倎値兤亖倱倝値兤 丂丂丂丂丂們倧倱兤 侾亄倲倎値2兤亖丂侾丂丂 丂丂丂丂丂丂丂 們倧倱2兤
摿偵忋偺侾丆俀斣栚偺岞幃偼廳梫偱偡丅
栤戣 兤偑撦妏偱倱倝値兤亖係乛俆偺偲偒丄們倧倱兤丆倲倎値兤傪媮傔傛 夝摎 倱倝値2兤亄們倧倱2兤亖侾丂傛傝 侾俇丂亄丂們倧倱2兤丂亖侾 俀俆 們倧倱2兤亖 俋 丂丂丂丂丂俀俆 們倧倱兤亖丂亅俁丂丂丂丂丂丂(兤偑撦妏側偺偱們倧倱兤亙侽) 丂丂丂丂丂丂丂俆 倲倎値兤亖倱倝値兤亖亅係 丂丂丂丂丂們倧倱兤丂丂俁
![]()
 塃恾偺傛偆側嶰妏宍偑偁傝奜愙墌偺敿宎傪俼偲偡傞偲
塃恾偺傛偆側嶰妏宍偑偁傝奜愙墌偺敿宎傪俼偲偡傞偲
丂倎丂丂丂亖丂丂倐丂丂丂亖丂丂們丂丂丂亖丂俀俼 倱倝値俙丂丂丂倱倝値俛丂丂丂倱倝値俠
栤戣 倎亖併俁丂倐亖併俀丂俙亖俇侽搙丂偺偲偒俛傪媮傔傛 夝摎 丂丂倎丂丂亖俀俼丂傛傝 倱倝値俇侽 俼亖侾 俀亖丂倐丂丂 丂丂倱倝値俛 倱倝値俛亖侾乛併俀 俛亖係俆丆侾俁俆 偙偙偱俛亄俠亖侾俀侽搙側偺偱丂俛亖係俆搙
![]()
 塃恾偺嶰妏宍偵偼師偺傛偆側娭學偺偁傝傑偡丅
塃恾偺嶰妏宍偵偼師偺傛偆側娭學偺偁傝傑偡丅
倎2亖倐2亄們2亅俀倐們cos俙 倐2亖們2亄倎2亅俀們倎cos俛 們2亖倎2亄倐2亅俀倎倐cos俠
偙傟傪曄宍偟偰師偺傛偆側岞幃傕懡梡偟傑偡丅
們倧倱俙亖倐2亄們2亅倎2 丂丂丂丂丂丂丂俀倐們
栤戣 倐亖俀丂們亖俁丂俙亖俇侽搙偺偲偒倎傪媮傔傛 夝摎 倎2亖倐2亄們2亅俀倐們cos俙 丂 亖俀2亄俁2亅俀丒俀丒俁丒侾乛俀 丂 亖係亄俋亅俇 丂 亖俈 倎亖併俈
![]()
 塃偺嶰妏宍偺柺愊偼師偺傛偆偵媮傑傝傑偡丅
塃偺嶰妏宍偺柺愊偼師偺傛偆偵媮傑傝傑偡丅
柺愊俽亖侾丂倐們sin俙 丂丂丂丂俀
栤戣 倎亖俁丂倐亖係丂們亖俆丂偺嶰妏宍偺柺愊傪媮傔傛 夝摎 們倧倱俙亖侾俇亄俀俆亅俋 丂丂丂丂丂丂俀丒係丒俆 丂丂丂丂亖丂俁俀丂亖丂係 丂丂丂丂丂丂係侽丂丂丂俆丂丂丂 倱倝値俙亖俁乛俆 俽亖侾丂倐們sin俙丂亖侾丂係丒俆丂俁 丂丂俀丂丂丂丂丂丂丂 俀丂丂丂丂丂俆 丂亖俇
堦斒偵偼丂値両丂偲彂偒傑偡丅
偙傟偼丄値亊(値亅侾)亊(値亅俀)亊丒丒丒亊侾丂偲偄偆堄枴偱偡丅
栤戣 俇両傪媮傔傛 夝摎 俇仏俆仏係仏俁仏俀仏侾亖俈俀侽
![]()
乵俙乶乵俛乶乵俠乶偐傜俀岅慖傫偱岅嬪傪嶌傞応崌俁亊俀捠傝偺曽朄偑偁傝傑偡丅
偙偺偙偲傪婰崋俹(僷乕儈僱乕僔儑儞)傪巊偭偰
3俹2
偲彂偒傑偡丅堄枴偼俁偮偺傕偺偐傜俀偮傪慖傇丄応崌偺悢偱偡丅
偙偙偱偼岅嬪偵弴斣偑偁傞偺偱俙俛偲俛俙偼嬫暿偟傑偡丅 堦斒偵
n俹r
偼丄値屄偺拞偐傜倰屄傪弴斣偵慖傇偲偒偺応崌偺悢傪昞偟丄寁嶼偼
n俹r亖値亊(値亅侾)亊丒丒丒(値亅倰亄侾)
偺傛偆偵倰夞偐偗嶼傪偡傞偲偄偆堄枴偱偡丅
栤戣 6俹3丂傪媮傔傛 夝摎 俇仏俆仏係亖侾俀侽
![]()
乵俙乶乵俛乶乵俠乶偐傜俀岅慖傫偱慻傪嶌傞応崌俁捠傝偺曽朄偑偁傝傑偡丅
偙偺偙偲傪婰崋俠(僐儞價僱乕僔儑儞)傪巊偭偰
3俠2
偲彂偒傑偡丅堄枴偼俁偮偺傕偺偐傜俀偮傪慖傃丄慻傪嶌傞応崌偺悢偱偡丅
偙偙偱偼俙俛偲俛俙偼摨堦側傕偺偱偡丅堦斒偵
n俠r
偼丄値屄偺拞偐傜倰屄傪慻偵偡傞偲偒偺応崌偺悢傪昞偟丄寁嶼偼
n俠r亖n俹r 丂丂 倰両
栤戣 6俠3丂傪媮傔傛 夝摎 俇亊俆亊係亖俀侽 俁亊俀亊侾