![]()
![]()
| 侾丆悢偲幃 | 場悢暘夝丂巜悢丂桳棟壔丂俀廳崻崋 |
| 俀丆悢楍 | 摍嵎悢楍丂摍斾悢楍丂奒嵎悢楍丂慟壔幃丂悢妛揑婣擺朄 |
| 俁丆暯柺婔壗 | 撪暘丂奜暘丂儊僱儔僂僗偺掕棟丂僠僃僶偺掕棟 |
拞妛峑帪戙偵傕場悢暘夝傪傗偭偨偲巚偆偺偱偡偑崅峑偱偼俁師幃傑偱埖偄傑偡丅
(倎亄倐)3亖倎3亄俁倎2倐亄俁倎倐2亄倐3 (倎亅倐)3亖倎3亅俁倎2倐亄俁倎倐2亅倐3 (倎亄倐)(倎2亅倎倐亄倐2)亖倎3亄倐3 (倎亅倐)(倎2亄倎倐亄倐2)亖倎3亅倐3
俀師幃傪場悢暘夝偡傞偲偒倶2偺學悢偑侾埲奜偺偲偒師偺偨偡偒妡偗傪巊偆偲曋棙偱偡丅
倎們倶2亄(倎倓亄倐們)倶亄倐倓 倎丂乢乛丂倐丂仺丂倐們 們丂乛乢丂倓丂仺丂倎倓 丂 倎們丂丂丂倐倓丂倎倓亄倐們 (倎倶亄倐)(們倶亄倓)
偙傟偑惉傝棫偮傛偆偵倎丆倐丆們丆倓傪寛傔傟偽偄偄傢偗偱偡丅
栤戣 俀倶2亄俁倶亄侾丂傪場悢暘夝偣傛 夝摎 倶2偺學悢偱偐偗偰俀偵側傞偺偼侾偲俀偺慻 掕悢崁偱偐偗偰侾偵側傞慻偼侾偲侾丂丂亅侾偲亅侾 侾丂侾仺丂俀 俀丂侾仺丂侾丂 俀丂侾丂俀亄侾 嵟屻偵偙偺偨偡偒妡偗偱榓偑俁偵側傞偺偼 倎亖侾丂倐亖侾丂們亖俀丂倓亖侾丂側偺偱 (倶亄侾)(俀倶亄侾)
![]()
巜悢偵偼埲壓偺婎杮揑側岞幃偑偁傝傑偡丅
倎m倎n亖倎m+n 乮倎m乯n亖倎mn 乮倎倐乯n亖倎n倐n
栤戣 (倎倐-1)3亊倎-4亐倎-2丂傪寁嶼偣傛 夝摎 倎3倐-3倎-4+2 亖倎3-4+2倐-3 亖倎倐-3
![]()
暘悢偺暘曣偵偼暯曽崻偑偁傞偲傛偔側偄偺偱桳棟壔偟傑偡丅
桳棟壔偺傗傝曽偼丄暯曽崻偑扨撈偱偁傞応崌偵偼丄偦偺悢傪
暘巕丄暘曣偵偐偗傑偡丅
栤戣 俁 丂傪桳棟壔偣傛 併俇 夝摎 俁丂亊丂併俇丂亖丂俁併俇亖併俇 併俇 亊丂併俇丂丂丂丂俇丂丂 俀
傕偟丄暘曣偑丂倎亄併倐丂偺宍偵側偭偰偄傞偲偒偼
暘曣暘巕偵倎亅併倐丂傪偐偗傑偡丅偡傞偲暘曣偐傜暯曽崻偑側偔側傝傑偡丅
栤戣 併俆亄併俀丂傪桳棟壔偣傛 併俆亅併俀 夝摎 (併俆亄併俀)(併俆亄併俀)丂亖丂俆亄俀亄俀併10 (併俆亅併俀)(併俆亄併俀)丂丂丂丂俆亅俀 亖俈亄俀併10 丂丂丂俁
![]()
崻崋偺拞偵崻崋偑偁傞偲偒丄師偺傛偆偵偡傞偙偲偑偱偒傑偡丅
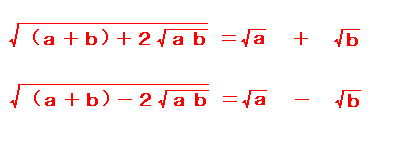
埲壓偱偼(倎亄丒丒丒)1/2偲偄偆昞尰傪偟偰偄傑偡偑偙傟傕
暯曽崻偺堦庬偱偡丅(俫俹偱偼昞偣側偄偺偱偙偺傛偆偵偟傑偟偨丅)
栤戣 (侾俀亅俇併俁))1/2丂傪娙扨偵偣傛 夝摎 丂乷俁(係亅俀併俁))乸1/2 亖併俁乷併俁亅侾乸 亖俁亅併俁
悢楍偼悢偑堦掕偺婯懃偱暲傫偱偄傑偡丅
偨偲偊偽俀丆俁丆俆丆俈丆侾侾丆侾俁丆侾俈丆侾俋丒丒丒偲偄偆偺偼
侾偲偦偺悢偟偐栺悢傪帩偨側偄偲偄偆慺悢偺廤傑傝偱偡丅
堦斒偵悢楍偼弴斣偵倎1丆倎2丆倎3丒丒丒偲偄偆傛偆偵昞偟傑偡丅
![]()
摍嵎悢楍偲偼悢楍偺嵎偑堦掕偺悢楍偺偙偲偱偡丅
偨偲偊偽侾丆係丆俈丆侾侾丒丒偲偄偆偺偼嵎偑俁偱偡丅
堦斒偵偼師偺傛偆偵側傝傑偡丅
倎n亖倎1亄(値亅侾)倓 丂丂倓丗岞嵎
栤戣 摍嵎悢楍丂俀丆俆丆俉丆丒丒丒偺堦斒崁倎n偲戞俀侽崁傪媮傔傛 夝摎 倎1亖俀 倓亖俁丂側偺偱 倎n亖俀亄俁(値亅侾) 丂 亖俁値亅侾 倎20亖俆俋
俽n亖倎1亄倎2亄丒丒丒倎n
偲俽n傪掕媊偟傑偡丅偙偺俽n傪乽榓悢楍乿偲偄偄傑偡丅
摍嵎悢楍偺榓偼師偺傛偆偵側傝傑偡丅
俽n亖侾値乷俀倎1亄乮値亅侾乯倓乸 丂 丂俀 丂 亖侾値乷倎1亄倎n乸 丂 丂俀
![]()
摍斾悢楍偼仮攞丄仮攞丒丒丒偲攞憹偟偰偄偔悢楍偺偙偲偱偡丅
偨偲偊偽丄侾丆亅俀丆係丆亅俉丆侾俇丆亅俁俀丒丒丒偲偄偆偺傕摍斾悢楍偱偡丅
倎n亖倎1倰n-1
偱昞偣傑偡丅倰偼岞斾偱偡丅
栤戣 摍斾悢楍1,-4,16,-64丒丒偺堦斒崁傪媮傔傛 夝摎 倎1亖侾 倰亖亅係 倎n亖(亅係)n-1
俽n亖倎1乮倰n亅侾乯 丂丂丂丂倰亅侾 偨偩偟丄倰亖侾偺偲偒偼 俽n亖値倎1
栤戣 倎n亖(亅係)n-1偱俆崁傑偱偺榓傪媮傔傛 夝摎 倎1亖侾 倰亖亅係丂丂側偺偱 俽n亖乮(亅係)n亅侾乯 丂丂丂亅係亅侾 丂亖侾亅(亅係)n 丂丂丂丂俆
![]()
奒嵎悢楍偼悢楍偺嵎偺悢楍偺偙偲偱偡丅
偨偲偊偽侾丆俀丆係丆俈丆侾侾丆侾俇丆俀俀丒丒丒偺嵎偼
侾丆俀丆俁丆係丆俆丆俇丒丒丒偵側偭偰偄傑偡丅
偙偺悢楍偺偙偲傪奒嵎悢楍偲偄偆傢偗偱偡丅
偄傑丄奒嵎悢楍傪倐n偲偡傞偲倎n偼師偺傛偆偵媮傑傝傑偡丅
倎n亖倎1丂亄丂嚁(k=1仺n-1)丂倐k
偙偙偱拲堄偟偨偄偺偼嚁偼n-1傑偱偟偐壛嶼偟側偄偲偄偆偙偲偱偡丅
栤戣 侾丆係丆侾侾丆俀俀丆俁俈丆俆俇丒丒丒偺堦斒崁傪媮傔傛 夝摎 倐n亖倎n+1亅倎n丂偲偍偔偲 倐n亖俁丆俈丆侾侾丆侾俆丆侾俋丂偲偄偆摍嵎悢楍偵側偭偰偄傑偡丅 倐1亖俁 倓 亖係丂丂側偺偱 倐n亖係値亅侾 倎n亖侾亄嚁倐k 丂 亖侾丂亄丂値(値亅侾)丂亅丂侾(値亅侾) 丂丂丂丂丂 丂丂 丂俀 丂 亖値2丂亅俁値丂亄丂俀 丂 丂俀丂丂 俀
![]()
崱傑偱丄悢楍偼丄倎n亖n2+n+3偺傛偆偵梌偊傜傟偨偺偱
n=3側偳偲戙擖偡傞偲丄倎3亖15偺傛偆偵偡偖偵傢偐傝傑偟偨丅
偟偐偟丄倎n+1亖3倎n+1丂偺傛偆偵偦傟埲慜偺崁傪梡偄偰昞偟偨偲偒偵
偙偺悢楍傪乽慟壔幃乿偲偄偄傑偡丅
慟壔幃偼丄偄偢傟傕娙扨側悢楍偵帩偭偰偄偔偙偲偱夝偔偙偲偑偱偒傑偡丅
偙偺悢楍傊偺抲偒姺偊曽朄偵偼僷僞乕儞偑偁傞偺偱丄偦傟傜傪妎偊傞偲偄偄偲巚偄傑偡丅
偍偙偙偱偼丄婎杮揑側僷僞乕儞傪徯夘偟傑偡丅
倎n+1丄倎n偺學悢偑侾偱偁傞僷僞乕儞偱偡丅
偙傟偼丄岞嵎俁偺摍嵎悢楍側偺偱丄偡偖偵夝偔偙偲偑偱偒傑偡丅
慟壔幃偱傕偭偲傕堦斒揑側幃偱偡丅
偙偺応崌丄x偺俀師曽掱幃偺傛偆偵偟偰夝偔曽朄偑偁傝傑偡丅
倎n+1-2倎n-3 = 0
x2-2x-3=0丂x=-1,3
偙偙偱偼丄x=3傪梡偄偰丄bn=an+3偲偄偆傛偆偵bn傪掕媊偟傑偡丅
偡傞偲丄倎n+1-2倎n-3 = 0偺幃偑bn+1-2bn=0偺幃傊曄傢傝傑偡丅
偙傟偼丄摍斾悢楍側偺偱bn傪媮傔傞偙偲偑偱偒傑偡丅
bn偑傢偐傟偽an偑傢偐傝傑偡丅
悢楍埲奜偵丄曄悢n傪娷傫偱偄傞僷僞乕儞偱偡丅
偙偺応崌偼丄奒嵎悢楍bn=倎n+1-倎n傪掕媊偟傑偡丅
偦偟偰丄n偺抣傪1偮偩偗偢傜偟偰嵎傪偲傝傑偡丅
| 倎n+1 | =2倎n | +n | -1 | |
| -) | 倎n | =2倎n-1 | +(n-1) | -1 |
(倎n+1-倎n)=2(倎n-倎n-1)+1
bn=2bn+1
偙偺偁偲偺夝偒曽偼丄忋偺僷僞乕儞偲乆偱偡丅
![]()
悢妛偺徹柧偵偼丄廬棃偼墘銏朄偲偄偆徹柧曽朄傪梡偄偰偒傑偟偨丅
偙傟偼丄弴斣偵忦審側偳傪媮傔丄嵟廔揑側掕棟傪媮傔傞偲偄偆曽朄偱偟偨丅
偟偐偟丄婣擺朄偱偼弴彉偑媡偵側傝傑偡丅
嵟弶偵徹柧偡傋偒掕棟偑惓偟偄偲偟丄偦傟傪巊梡偟偰傕柕弬偑側偗傟偽
惓偟偐偭偨偲偡傞曽朄偱偡丅
埲壓偵丄悢妛揑婣擺朄傪帵偟傑偡丅
| 悢妛揑婣擺朄 帺慠悢値偵娭偡傞柦戣偵偮偄偰 [1]丂値亖侾偺偲偒丄柦戣偑惉傝棫偮 |
偙傟偼丄[1]偱n=1偲偄偆嵟弶偺忬懺偱幃偑惉傝棫偭偰偄傞偙偲傪帵偟
[2]丄[3]偱n=k偺偲偒偵惉傝棫偭偰偄傞偲丄堦偮忋偺n=k+1偱傕惉傝棫偮偙偲傪帵偟傑偡丅
偡傞偲丄n=1偱惉傝棫偪丄堦偮忋偺n=2偱傕惉棫丄n=3偱傕n=4偱傕丒丒丒
偲偄偆嬶崌偵偡傋偰偺帺慠悢偱惉傝棫偮偙偲偵側傝傑偡丅
栤戣
1+2+22+丒丒丒2n-1=2n-1丂傪徹柧偣傛
夝摎
[1]丂n=1偺偲偒丄20=21-1丂偑惉傝棫偮
[2]丂n=k偺偲偒1+2+22+丒丒丒2k-1=2k-1偑惉傝棫偮偲偡傞偲
[3]丂n=k+1偺偲偒丄
(嵍曈)亖1+2+22+丒丒丒2k-1+2k
(塃曈)亖2k+1-1亖2k+2k-1
偄偢傟傕丄椉曈偵2k偑壛嶼偝傟偰偄傞偺偱
n=k+1偺偲偒偱傕摍幃偑惉棫偡傞丅
傛偭偰丄1+2+22+丒丒丒2n-1=2n-1偑惉傝棫偮
慄暘俙俛傪侾丗俀偵撪暘偡傞揰俹偑偁傞帪恾偺埵抲偵俹偑偁傝傑偡丅
A-----------P--------------------------B
1 2
堦斒偵俙(x1,y1)偲俛(x2,y2)偑俹偵傛偭偰倣丗値偵撪暘偝傟傞偲偒
俹偺倶乮倷乯嵗昗偼師偺傛偆偵側傝傑偡丅
倃亖値倶1丂亄丂倣倶2 丂丂丂 倣丂亄丂値 倄亖値倷1丂亄丂倣倷2 丂丂丂 倣丂亄丂値
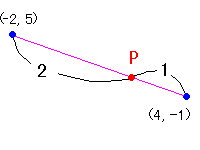
栤戣 俙(亅俀丆俆)丂俛(係丆亅侾)偑偁傞偲偒丄 俀丗侾偵撪暘偡傞揰偺嵗昗傪媮傔傛 夝摎 倃亖俀丒係亄侾丒(亅俀) 丂丂丂俀丂亄丂侾 丂亖俀 倄亖俀丒(亅侾)亄侾丒俆 丂丂丂丂丂俀丂亄丂侾 丂亖侾 傛偭偰丄乮俀丆侾乯
![]()
撪暘偼揰俹偑慄暘俙俛撪偵偁傞応崌偺偙偲側偺偱偡偑
奜暘偼慄暘俙俛偺奜偵偁傞応崌偺偙偲偱偡丅
奜暘揰傪媮傔傞偲偒偼丄愭傎偳偺岞幃傪棙梡偟傑偡丅
乽倣丗値偵奜暘乿偲偄偆偲偒偼偳偪傜偐堦曽偺晞崋傪斀揮偡傞偙偲偱
懳墳偱偒傑偡丅
栤戣 俙(亅俀丆俆)丂俛(係丆亅侾)偑偁傞偲偒丄俀丗侾偵奜暘偡傞揰偺嵗昗傪媮傔傛 夝摎 俀丗侾偵奜暘偲偼丄俀丗亅侾偵撪暘偲偄偆偙偲側偺偱 倃亖俀丒係亅侾丒(亅俀) 丂丂丂俀丂亅丂侾 丂亖侾侽 倄亖俀丒(亅侾)亅侾丒俆 丂丂丂丂丂俀丂亅丂侾 丂亖亅俈 傛偭偰丄乮侾侽丆亅俈乯
![]()
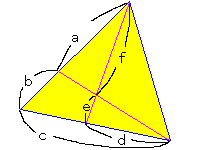 塃恾偺傛偆側屜偺傛偆側嶰妏宍偱偼
塃恾偺傛偆側屜偺傛偆側嶰妏宍偱偼
乽儊僱儔僂僗偺掕棟乿傪棙梡偡傞偙偲偑偱偒傑偡丅
儊僱儔僂僗偺掕棟偼嶰妏宍偺斾傪傕偲傔傞偲偒偵旕忢偵曋棙偱偡丅
倎丂們丂倕丂亖丂侾 倐丂倓丂倖
偙偺斾偺偲傝偐偨偼彮偟暋嶨側偺偱拲堄偟偰偔偩偝偄丅
![]()
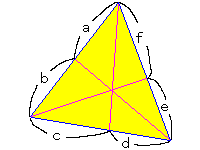 僠僃僶偺掕棟偼儊僱儔僂僗偺掕棟傪奼挘偟偨傕偺偱偡丅
僠僃僶偺掕棟偼儊僱儔僂僗偺掕棟傪奼挘偟偨傕偺偱偡丅
塃恾偺傛偆側懳徧揑側嶰妏宍偵棙梡偟傑偡丅
岞幃帺恎偼曄傢傝傑偣傫偑丄斾偺偲傝偐偨偑
愭傎偳偲曄傢傝丄偒傟偄側宍傪偟偰偄傑偡丅
倎丂們丂倕丂亖丂侾 倐丂倓丂倖