![]()
![]()
| 侾丆恾宍偲幃 | 嫍棧丂墌偲捈慄丂墌偺愙慄丂椞堟 |
| 俀丆嶰妏娭悢 | 儔僕傾儞丂僌儔僼丂壛朄掕棟丂榓愊曄姺岞幃丂嶰妏娭悢偺崌惉 |
| 俁丆巜悢偲懳悢 | 椵忔崻丂巜悢娭悢丂懳悢丂懳悢娭悢 |
悢俀暘栰偺旝暘愊暘偼悢俁偺儁乕僕偵嵹偭偰偄傑偡丅
捈慄倎倶亄倐倷亄們亖侽偲嵗昗(倶丆倷)偲偺嫍棧偼師偺傛偆偵側傝傑偡丅
乥倎倶亄倐倷亄們乥 丂丂(倎2亄倐2)1/2
![]()
墌偲捈慄偺曽掱幃偼堦斒偵偼師偺傛偆偵媮傑傝傑偡丅
(倶亅倫)2亄(倷亅倯)2亖倰2 倎倶亄倐倷亄們亖侽
嵟弶偺墌偺幃偼丄嵗昗乮倫丆倯乯傪拞怱偲偡傞敿宎倰偺墌偺曽掱幃偱偡丅
俀斣栚偺曽掱幃偼拞妛峑帪戙偵倷亖倎倶亄倐傪傛傝堦斒偵偟偨傕偺偱偡丅
偙傟偵傛偭偰倶亖俆偺傛偆側捈慄傕昞偣傞傛偆偵側傝傑偟偨丅
![]()
 倶2亄倷2亖倰2丂偺墌忋偺嵗昗乮倶侾丆倷侾乯傪
倶2亄倷2亖倰2丂偺墌忋偺嵗昗乮倶侾丆倷侾乯傪
捠傞愙慄偺幃偼師偺傛偆偵側傝傑偡丅
倶1倶亄倷1倷亖倰2
墌偲捈慄偑愙偟偰偄傞偐岎傢偭偰偄傞偺偼偲偄偆偙偲偼
墌偺曽掱幃偲捈慄偺曽掱幃傪楢棫偝偣偰堦偮偺幃偵偟傑偡丅
偦偙偱敾暿幃傪棙梡偡傟偽偄偄傢偗偱偡丅
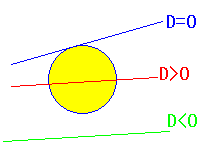
俢亖侽側傜偽愙偟偰偄偰丄俢亙侽側傜偽岎傢傝傑偣傫丅
俢亜侽偱偼俀揰偱岎傢傝傑偡丅
![]()
崱傑偱丄倷亖倖乮倶乯偺宍偱偼丄偁傞堦揰傪寛傔偰偄傑偟偨丅
椞堟偼丄倷亙倖乮倶乯偺傛偆偵晄摍崋偱昞偟傑偡丅
偨偲偊偽丄倷亙倶亄俀偱偼丄倷亖倶亄俀傛傝壓懁(倷幉偺晧偺曽岦)慡懱偑椞堟偵側傝傑偡丅
椞堟偱偼丄暋悢偺忦審傪壽偡偙偲偑壜擻偱
倷亙倶亄俀 倶亜侽 倷亜侽
偲偄偆忦審偑偁傞偲(0,0),(2,0),(0,2)傪捠傞捈妏嶰妏宍偑椞堟偲側傝傑偡丅
崱傑偱丄妏搙傪昞偡偺偵偼搙悢朄傪梡偄偰偒傑偟偨丅
偡傞偲丄侾廃偼俁俇侽搙偵側傝傑偡丅
偟偐偟丄暿偺傕偭偲曋棙側昞尰曽朄偑偁傝傑偡丅偦傟偑儔僕傾儞偱偡丅
搙悢朄偱偼乽亱乿偲偄偆扨埵偑偄偨偺偱偡偑丄儔僕傾儞偱偼偁傝傑偣傫丅
儔僕傾儞偱偼丄侾廃偑俀兾偵側傝傑偡丅
搙悢朄偲儔僕傾儞偵偼埲壓偺娭學偑偁傝傑偡丅
侾亱亖丂兾丂 丂丂丂侾俉侽
| 搙(亱) | 侽 | 俁侽 | 俇侽 | 俋侽 | 侾俉侽 |
| 儔僕傾儞 | 侽 | 兾乛俇丂 | 兾乛俁 | 兾乛俀 | 兾 |
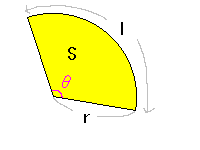
儔僕傾儞傪梡偄傞偙偲偱師偺傛偆側傕偺偑娙扨偵媮傑傝傑偡丅 塃恾偺墌廃倢偼
倢亖倰兤丂丂丂丂倢丗墌廃 俽亖侾倰2兤 丂丂俽丗柺愊 丂丂俀
![]()
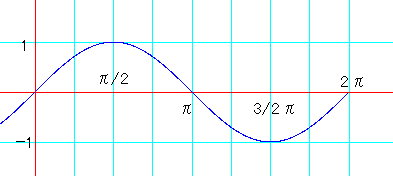
倷亖倱倝値兤丂偺僌儔僼偼忋恾偺傛偆偵側傝傑偡丅
倷亖們倧倱兤丂偼丂倷亖倱倝値(兤丂亄丂兾乛俀)偵曄宍偱偒傞偺偱
倷亖倱倝値兤丂偺僌儔僼傪兤曽岦偵亅兾乛俀偩偗堏摦偟偨傕偺偵側傝傑偡丅
倷亖俙倱倝値兤丂偺僌儔僼偼丂倷亖倱倝値兤傪倷幉曽岦偵俙攞偟偨傕偺偵側傝傑偡丅
倷亖倱倝値(俙兤)丂偼倷亖倱倝値兤傪兤曽岦偵懳偟偰侾乛俙攞偟偨傕偺偵側傝傑偡丅
栤戣 倷亖俀們倧倱(俀兤丂亄丂兾乛俀)丂偺僌儔僼傪偐偗 夝摎俀們倧倱(俀兤丂亄丂兾乛俀)丂亖丂亅俀倱倝値俀兤 偙傟偼丄倱倝値兤偺僌儔僼傪忋壓斀揮偝偣丄俀攞偟偨傕偺傪 兤曽岦偵侾乛俀攞偟偨傕偺側偺偱埲忋偺傛偆偵側傝傑偟偨丅
![]()
埲壓偺岞幃偼旕忢偵廳梫側岞幃偱丄壛朄掕棟偲偄傢傟偰偄傑偡丅
倱倝値(兛亄兝)亖倱倝値兛 們倧倱兝丂亄丂們倧倱兛 倱倝値兝 倱倝値(兛亅兝)亖倱倝値兛 們倧倱兝丂亅丂們倧倱兛 倱倝値兝 們倧倱(兛亄兝)亖們倧倱兛 們倧倱兝丂亅丂倱倝値兛 倱倝値兝 們倧倱(兛亅兝)亖們倧倱兛 們倧倱兝丂亄丂倱倝値兛 倱倝値兝
傑偨丄偙傟傜傪梡偄傞偙偲偵傛偭偰倲倎値(兛亇兝)傕媮傑傝傑偡丅
倲倎値(兛亄兝)亖丂倲倎値兛丂亄丂倲倎値兝 丂丂丂丂丂丂丂丂侾丂亅丂倲倎値兛 倲倎値兝 倲倎値(兛亅兝)亖丂倲倎値兛丂亅丂倲倎値兝 丂丂丂丂丂丂丂丂侾丂亄丂倲倎値兛 倲倎値兝
壛朄掕棟偱兛亖兝偲偡傞偙偲偵傛偭偰俀攞妏偺岞幃偑摼傜傟傑偡丅
倱倝値(俀兛)亖俀倱倝値兛 們倧倱兛 們倧倱(俀兛)亖們倧倱2兛丂亅丂倱倝値2兛 丂丂丂丂丂丂亖侾丂亅丂俀倱倝値2兛 丂丂丂丂丂丂亖俀們倧倱2兛丂亅丂侾
俀攞妏偺岞幃傪媡偵棙梡偡傟偽敿妏偺岞幃偑媮傑傝傑偡丅
倱倝値2(兛/2)丂亖丂侾丂亅丂們倧倱兛 丂丂丂丂丂丂丂丂丂丂丂丂俀 們倧倱2(兛/2)丂亖丂侾丂亄丂們倧倱兛 丂丂丂丂丂丂丂丂丂丂丂丂俀
![]()
壛朄掕棟傪巊偭偰嶰妏娭悢偺愊傪榓偵曄姺偡傞偙偲偑偱偒傑偡丅
傑偨丄斀懳偵榓傪愊偵曄姺偡傞偙偲傕偱偒傑偡丅
![]()
倱倝値兤偲們倧倱兤偺榓傪傑偲傔傞偙偲偑偱偒傑偡丅
俙倱倝値兤丂亄丂俛們倧倱兤丂亖丂(俙2亄俛2)1/2丂倱倝値(兤亄兛) 偨偩偟丄 們倧倱兛亖丂丂俙丂丂丂 丂丂丂丂丂(俙2亄俛2)1/2 倱倝値兛亖丂丂俛丂丂丂 丂丂丂丂丂(俙2亄俛2)1/2
栤戣 併俁倱倝値兤丂亅丂們倧倱兤丂傪娙扨偵偣傛 夝摎 俙2亄俛2亖倃丂偲偡傞偲 俙亖併俁丂丂俛亖亅侾丂傛傝丂倃亖俀 們倧倱兛亖併俁丂丂丂倱倝値兛亖亅侾 丂丂丂丂丂丂俀丂丂丂丂丂丂丂丂丂俀 兛亖亅兾乛俇 傛偭偰(梊幃)亖俀倱倝値(兤亅兾/6)
椵忔崻偼儖乕僩偺慜偵彫偝側悢帤偑偮偄偰偄傑偡丅
偙傟偼丄巜悢偲師偺傛偆側娭學偑偁傝傑偡丅
(n併倎)m丂亖倎m/n
栤戣 3併250丂丂傪娙扨偵偣傛 3併俀 夝摎 丂(250)1/3丂亊丂俀-1/3 亖俀1/3丂亊丂俆丂亊丂俀-1/3 亖俆
![]()
巜悢娭悢偼堦斒偵師偺傛偆偵偐偒傑偡丅
倷亖倎x
偙偺偲偒丄僌儔僼偼師偺傛偆偵側傝傑偡丅
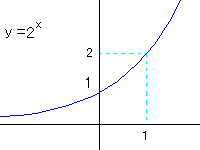 倷幉忋偱偼侾傪捠傝丄倶偺晧偺曽岦偱偼倶幉傊偺慟嬤慄偵側傝傑偡丅
倷幉忋偱偼侾傪捠傝丄倶偺晧偺曽岦偱偼倶幉傊偺慟嬤慄偵側傝傑偡丅
倶亖侾偱偼倷偼倎偵側傝傑偡丅(塃恾偱偼倎亖俀側偺偱(1,2)傪捠傞)
偨偩偟丄倎亜侽偱偁傞昁梫偑偁傝傑偡丅
倷亖倎-x
偙偺偲偒偼巜悢偺僌儔僼偼倷幉懳徾偵側傝傑偡丅
倷亖倎bx
偙偺偲偒偼丄倎x傪倶幉偺曽岦偵侾乛倐攞偟偨傕偺偵側傝傑偡丅
栤戣侾 俀x亙俉丂傪夝偗 夝摎侾 俀x亙俀3 俀亜侾側偺偱巜悢晹暘傪扨弮偵斾妑偱偒 倶亙俁 栤戣俀 乛侾乢2x丂亜 侾 丂丂丂丂傪夝偗 乢俁乛丂丂丂 俉侾 夝摎俀 乛侾乢2x丂亜 乛侾乢4 乢俁乛丂丂丂 乢俁乛 1/3亙侾丂側偺偱晄摍崋傪擖傟懼偊偰 俀倶亙係 丂倶亙俀
![]()
俀x亖俁
偲偄偆娭學偑偁傞偲偒
倶亖倢倧倗2俁
偲彂偒捈偣傑偡丅偙偺倢倧倗偲偄偆偺偑懳悢偱偡丅堦斒偵偼
俼亖倎r丂丂丂仼仺丂丂倰亖倢倧倗a俼
偨偩偟丄倎亜侽丂俼亜侽丂倎亗侾丂偲偄偆忦審偑偁傝傑偡丅
偙偺偲偒丄俼傪乽恀悢乿丄a傪乽掙乿偲偄偄傑偡丅
倢倧倗偵偼師偺惈幙偑偁傝傑偡丅
倢倧倗a俼俽亖倢倧倗a俼丂亄丂倢倧倗a俽 倢倧倗a俼乛俽亖倢倧倗a俼丂亅丂倢倧倗a俽 倢倧倗a俼p亖倫倢倧倗a俼
倢倧倗a侾亖侽 倢倧倗a倎亖侾
栤戣 倢倧倗5俈俆亅倢倧倗5侾俆丂丂傪寁嶼偣傛 夝摎 (梊幃)亖倢倧倗5俈俆乛侾俆 丂丂丂亖倢倧倗5俆 丂丂丂亖侾
掙偺悢偼乽掙偺曄姺岞幃乿偵傛偭偰曄偊傞偙偲偑偱偒傑偡丅
倢倧倗a俼亖倢倧倗b俼 丂丂丂丂丂 倢倧倗b倎
![]()
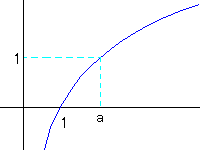 懳悢娭悢偼巜悢娭悢傪倷亖倶偱懳徾偵偟偨傛偆側宍傪偟偰偄傑偡丅
懳悢娭悢偼巜悢娭悢傪倷亖倶偱懳徾偵偟偨傛偆側宍傪偟偰偄傑偡丅
倷亖倢倧倗a倶丂偑偁偭偨偲偒丄倶偼倶亜侽偲偄偆惂栺傪庴偗傑偡丅
倶亖侾偱偼倷亖侽偵側傝丄倶亖倎偱偼倷亖侾偵側傝傑偡丅
栤戣 俀30丂偺寘傪媮傔傛 夝摎 倢倧倗10 俀30 亖俁侽倢倧倗10 俀 亖俁侽亊0.3010亖俋丏侽俁侽 俋亙倢倧倗10 俀30亙侾侽 侾侽9亙俀30亙侾侽10 傛偭偰俀30偼侾侽寘偵側傝傑偡丅