![]()
![]()
| 1,ゼミについて | |
| 2,化学結合 | 量子状態 結合 混成軌道 その他の結合 |
| 3,結晶構造 | 結晶格子 対称性 主な結晶構造 |
研究室に配属されると、「ゼミ」というものがあります。
ゼミでは、参考書を1冊きめて、それをじっくりと分担して
ゼミを進めていくことになります。
私の研究室では、次のような本を使うことにしました。
本 名 固体物理学 出版社 シュプリンガー・フェアラーク東京株式会社 発行日 1998/1/15 価 格 定価3600円(税別) ページ 458ページ
この本は最近出たばかりのもので、書店に行くと下の棚に山積みになっています。
この本は結構厚いのですが、実験関係の記事や写真などがあって
結構読みやすいものになっています。
(しかし、ドイツ語を翻訳したものなので変な記号が使われていたり
するため内容説明などはキッテルの方が優れていると思います。)
原子の周りを回っている電子の状態は次の3つの量子変数で あらわすことができます。
原子の軌道を内側からn=1,2,3・・・としたものです。
たとえば、水素原子の電子はn=1の軌道を回っていることになります。
電子の軌道は、s軌道、p軌道、d、f・・などがあります。
これは、電子のもつ角運動量によって決まっています。
角運動量はlを使って表し、l=0では、s軌道、1ではp軌道
2でd、3でf・・・と決まっています。
実際の原子では、これらの2つの量子数を組み合わせて
エネルギー順位別に1s、2s、2p、3s、3p、4s、3d・・・
と詰まっていきます。
| 1s | H He |
| 2s | Li Be |
| 2p | B→Ne |
| 3s | Na Mg |
| 3p | Al→Ar |
| 4s | K Ca |
| 3d | Sc→Zn |
| 4p | Ga→Kr |
| 5s | Rb Sr |
| 4d | Y→Cd |

ここで注目してほしいのは、3d軌道が4s軌道の後に
4d軌道が5sの後にあります。これらの軌道にある原子は
「遷移元素」と呼ばれています。このようなことがおきる原因は
s軌道は球面なのに対し、p軌道、d軌道となるほど、軌道は
ゆがんできます。そのため、たとえば3d軌道は4s軌道の
外側にいってしまうことがあり、この間に別の電子が存在すると
原子とのクーロンポテンシャルが小さくなってしまうため
(これを、遮蔽効果といいます。)
エネルギー順位が逆転することがあるわけです。
いまのnとl以外にもmという量子数が存在します。
これは、「磁気量子数」というもので取りうる値は
m=−l、−l+1、・・・・l
の範囲です。(lは角運動量)
以上の3つの変数で電子の状態が決められます。
これ以外にも、電子のスピンというものがあります。
1つの量子状態に複数の電子が入れないという法則を
「パウリの排他律」といいます。
![]()
いままでは、単独の原子について考えてみました。
ここでは、原子が2つあった場合について考えてみましょう。
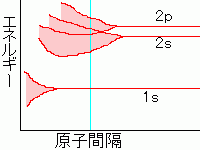
2つの原子間の距離をだんだん縮めていくと
原子同士の相互作用によって
電子のエネルギー順位が分裂します。
このとき、図のようにp軌道とs軌道が
エネルギー的に重なった
価電子帯(バレンスバンド)を形成します。
このように、原子間の距離を近づけるとエネルギーを
小さくすることができるのですが、原子間の反発力も
大きくなるので、これらがつりあったところで
平衡状態になります。(右図の青線)
この平衡状態になったときの波動関数の広がりによって
原子間の結合の種類が違ってきます。
波動関数があまり広がらないときはこの原子同士で
共有結合をします。
共有結合では、結合の強さは原子同士の距離だけではなく
方向にも依存するので「方向性結合」とも呼ばれます。
逆に、波動関数が遠くの原子まで作用するようになると
金属結合になるというわけです。
イオン結合では波動関数の広がりが小さいのですが
共有結合と違って方向性を持ちません。
![]()
いま、C(炭素)のダイヤモンド構造について考えてみましょう。
Cの電子軌道は2sが2個、2pが2個になっています。
単純に考えると、2p軌道の電子同士が結合することを
予想しますが、実際にはもっと安定な構造をとります。
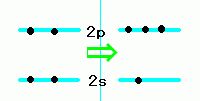
まず、2s軌道にあった電子の1つが2p軌道に上がります。
こうなると図に右側のようになります。
さらに、2s軌道の波動関数と2p軌道の波動関数が
重なって線形結合をして新しい波動関数を作ります。
これをsp3混成軌道といいます。
sp3混成軌道では、波動関数が4方向に伸びていて正四面体構造をとります。
また、波動関数は平行に重なるため強い共有結合をします。
これが、「ダイヤモンド構造」が強い理由です。

次にグラファイトについて考えてみましょう。
グラファイトもダイヤモンドと同じように炭素によってできています。
しかし、ダイヤモンドとは性質が異なっています。
グラファイトの場合も2s軌道から2p軌道に電子が
移ります。しかし、ここでsp3混成軌道を作らずに
2sの電子1つと2pの電子2つによってsp2混成軌道を
作ります。このとき、各々の波動関数は120°の角度を持ちます。
2p軌道には電子が1つ取り残されています。
グラファイトでは、sp2混成軌道の部分が強い共有結合になり
残りの電子は隣と2重結合(π結合)をします。
このため、平面方向には強い結合力があるのですが
平面間の結合力は弱いものになっています。
このsp2混成軌道は最近話題のC60もこの構造をとっています。
![]()
1つの水素原子が他の2つの原子に結合しているとき、水素結合といいます。
水素結合はファンデルワールス力と比べて強い結合力があり
1つの結合あたり0.1eV程度あります。
この結合はどの固体にも存在します。
この力は、原子内の電荷が零点運動によって揺らぎ
このときに生じる電気双極子モーメントが引き合うわけです。
結合エネルギーは0.1eV程度しかありません。
大半の結晶は原子は整然と並んでいます。
そこで結晶構造を考えるときは、原子は周期的に並んでいるものとして
格子欠陥は摂動論で解くことになります。
それに対して結晶構造が不規則で、周期性がないものを
「アモルファス」といいます。
![]()
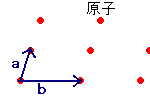
2次元の平面についての格子について考察するとき
右図のようにベクトルa、bを導入します。
このとき、a、bは単位ベクトルで、このベクトルによって
構成される平行四辺形の内部には1つの原子が存在します。
任意の格子点は次の式であらわせます。
rn=n1a + n2b
さらに、このベクトル同士のなす角をγとします。
これらを使って任意の2次元の結晶構造が表せます。
たとえば、γ=90°ならば長方格子、γ=90°,a=bでは
正方形、γ=60°,a=bでは六方格子になります。
さらに、3次元的にするため、ベクトルcとベクトル同士がなす角度
α、βを新たに導入します。そのときの結晶構造を以下の表にまとめます。
| 基底ベクトル | 角 | 結晶軸 |
| a≠b≠c | α≠β≠γ≠90° | 3斜 |
| a≠b≠c | α=γ=90°β≠90° | 単斜 |
| a≠b≠c | α=β=γ=90° | 斜方 |
| a=b≠c | α=β=γ=90° | 正方 |
| a=b≠c | α=β=90°γ=120° | 六方 |
| a=b=c | α=β=γ≠90° | 菱面体 |
| a=b=c | α=β=γ=90° | 立方 |
![]()
数学的には、x=−x、y=y、z=zで与えられる座標変換です。
鏡映面では、左右対称になっています。
数学的には、x=−x、y=−y、z=−zで与えられる座標変換です。
反転中心に関して点対称になっています。反転対称性を表す記号として
![]()
であらわします。
結晶を360°回転させたとき、n回同じ構造になったとき
「n次の回転軸がある」といいます。
たとえば、ベンゼン環の場合は6次の回転軸があり、60°ごとに
対象になっていることがわかります。
回転対称を表す記号として、「6」のように数字を直接書きます。
さらに、回転と反転を組み合わせて、nバーにすることもあります。
ここに、対象操作を指定する方法に「シェンフリースの記法」
というものがあります。
| 回転軸と 主鏡映面に よる分類 |
Cj | j次の回転軸 |
| Sj | j次の回反軸 | |
| Dj | j次の主回転軸とこれに垂直なj本の2回軸 | |
| T | 正四面体における4本の3回軸と3本の4回軸 | |
| O | 正八面体における4本の3回軸と3本の4回軸 | |
| Ci | 反転中心 | |
| Cs | 鏡映面 | |
| 鏡映面に 対する 付加的な 記号 |
h | 水平(主回転軸に垂直) |
| v | 垂直(主回転軸に平行) | |
| d | 対角的(2回転軸の2等分面内にある主回転軸に平行) |
たとえば、4次の回転軸を持つものでは、C4vで表すことができます。
![]()
次に、実際の結晶に多く見られる構造について考察します。
面心立方構造は、通常fcc構造と略されます。
これには、4本の3回軸と、4回軸に垂直な鏡映面を持ちます。
この構造を持つ金属は、Cu,Ag,Au,Ni,Alなどがあります。

右図で、緑色の原子をA、黄色をB、水色をC層
とするとfcc構造の原子の積み重なり方は
図のようなA→B→C→A→B→C・・・
というものが続きます。
六方最密構造は、通常hcp構造と略されます。
hcp構造では単位胞に2個の原子を含みます。
hcpでの原子の積み重なり方はfccに似ているのですが
A→B→A→B・・・のようにC層がありません。
この構造を持つ金属は、Zn、Mgなどがあります。
体心立方構造は、通常bcc構造と略されます。
bccでの原子の積み重なり方は2パターンで構成されます。
この構造を持つ金属は、Fe,Baなどがあります。