| １，バンド理論 | ブロッホの定理 束縛された電子 バンド |
| ２，磁性 | 磁化率 交換相互作用 交換相互作用２ |
今まで、結晶中の電子のモデルとして「自由電子気体モデル」を用いてきました。
しかし、これでは簡単すぎるためここでは、２つのアプローチをします。
ひとつは、実際の電子は今までのように気体のように振る舞うと考え
これに、原子核によるポテンシャルの影響を加味する方法が１つ。
もうひとつは自由電子は原子核に固定されているものとして考える方法です。
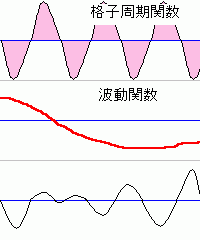
格子が規則的に間隔がａで並んでいる場合、
ポテンシャルは
ｕk(r)＝ｕk(r＋ａ)
となります。また、波動関数がΨで表されるとき
これらを重ね合わせたのが「ブロッホ波」というものです。
ブロッホ波は、格子周期関数と波動関数との
積で表すことができます。
ブロッホの定理では、電子は気体のように自由に振舞うと
仮定していました。しかし、ここでは、電子は
もともと原子核に束縛されていると考えてみます。
この電子の波動関数は空間上にひろがっています。
ここにさまざまな軌道をとっている電子の波動関数は
線形的に重なっていると考えられます。
これを「LCAO法」といいます。
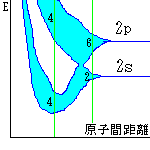この典型的な例が「混成軌道」です。
たとえばC (炭素)の場合、2ｓ軌道に２個、２ｐ軌道に
２個の電子が存在します。
この電子が原子核に近づくと、エネルギーが分裂をします。
もちろん、２ｓ軌道には２個、２ｐ軌道には６個の電子が
入ることができます。
しかし、ここで、２ｓ軌道の電子のうち1個が
２ｐ軌道に上がって、２ｓの電子１個と
２ｐの電子3個が結合してｓｐ３混成軌道を作ると
より安定します。
この状態は右図の左の状態になっているので
エネルギー的にはかなり安定します。
このため、エネルギー的にはかなり安定します。
ダイアモンドの場合、エネルギー状態の低いバンドは
すべて電子で埋められ、上のバンドとのエネルギーギャップも
大きいので、絶縁体として働きます。
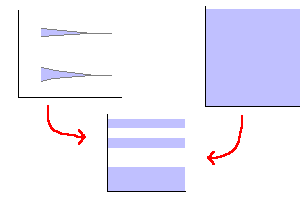エネルギーバンドに関するアプローチは２つ
ありました。
１つは、自由電子がもともと自由に分布している
ところにブラッグ反射によって、特定の領域が
占有できないことによってバンドが生じる
というものです。(図の右側)
２つめの考え方は、「束縛された電子」の節で
述べたようにもともと電子は原子核に束縛されて
いるものの電子同士が接近することによって
エネルギーが連続的になってエネルギーバンドが
生じるというものです。(図の左側)
物質に外部から磁場を加えると、自発磁化が生じます。
このとき、自発磁化は
Ｍ＝χＨo
で表すことができます。
このとき、χが負のものを「反磁性」といいます。
また、外部磁場をかけていなくても磁化を生じるものを
「強磁性」、χが正で外部磁場に比例して自発磁化を生じるものを
「常磁性」といいます。
一般にχは、常磁性項と反磁性部項の和になっています。
常磁性項は、電子の軌道やスピンの向きに関係しています。
反磁性項は、レンツの法則によって誘起された渦電流によるものです。
2つの電子が存在する場合を考えるために、水素分子の場合を考えます。
ここには、陽子が2個と、電子が2個存在します。
電子にそれぞれ1，2という番号をつけて、陽子にはＡ，Ｂという
文字をつけます。系全体のはハミルトニアンは
であらわせます。右辺の最後の項は、電子相互作用による
ハミルトニアンです。この項は微小なので無視して、
A,Bの陽子ごとに波動関数であらわして近似すると
次式の上が求まります。
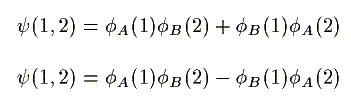
もし、電子のスピンまで考慮する場合は、電子同士お互いに
反平行になる必要があるので、そのときは下の式を用います。
次に、金属の自由電子間の交換相互作用について考えます。
同じ軌道の電子対に対する交換相互作用は、負になるので安定しますが
自由電子間では正になるので不安定です。
ある自由電子が上向きのスピンを持っていたとしましょう。
すると、交換相互作用によって、その電子の近傍には
同じ上向きのスピンを持った電子が存在する確率が小さくなります。
これを「交換ホール」といいます。
このホールは、電子の周りに1〜2Å程度の広がりがあります。
この電子は交換ホールを引きずって運動するので、近くに同じスピンを
持った電子が存在すると、正の交換相互作用のため、エネルギー的に損をします。
そのため、あたかも質量が増加したかのように振舞います。
このときの見かけ上の質量は「有効質量」といいます。
いま、簡単のために電子のスピンは上と下の２方向しかないと仮定します。
上向きの電子の個数をｎ↑、下向きをｎ↓でおき、Nを自由電子総数
E(ｋ)は、通常のバンドエネルギーです。
この式の、Iは、「ストーナーパラメーター」といい、電子相関によって
1電子あたりどれだけエネルギーが減少するかを表しています。
Rは、スピン方向の偏りをあらわしていて、0では偏りなし、非0で
偏りがあるので強磁性ということになります。
ここで、定数Rは正になるように上下スピンの方向を」定めるので
Ｒ＞０
が強磁性の条件ということになります。
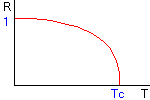
この定数Ｒと温度の関係をグラフにすると
右のようになります。
T>Tcでは、R=0となって常磁性体になっていますが
T<Tcでは、Rが有限となり強磁性であることがわかります。
Niでは、常温ではT<Tcなので強磁性となるので磁石などに
利用されています。しかし、温度を上げると磁荷が失われるのは
T>Tcなので常磁性体になってしまうためです。
上へ
Topに戻る