![]()
![]()
| 侾丆惷帴婥 | 婎杮朄懃丂帴婥憃嬌巕丂帴惈懱丂儅僋僗僂僃儖偺墳椡 |
| 俀丆揹帴桿摫 | 敪揹丂儘乕儗儞僣椡丂價僆乕僒乕僶儖偺朄懃丂傾儞儁乕儖偺朄懃揹巕夞楬 |
| 俁丆揹帴攇 | 儅僢僋僗僂僃儖曽掱幃丂揹帴攇丂摟夁丒斀幩 |
![]()
惷帴婥偼丄傎傏丄惷揹応偺岞幃傪帴婥偵曄偊傟偽偄偄偺偱偡丅
岅嬪傕丄偨偄偰偄偼揹仺帴偵曄偊傞偩偗偱偡丅嬶懱揑偵偼丄
丂丂揹奅丂俤仺帴奅丂俫 丂丂揹埵丂冇仺帴埵丂冇m 丂 桿揹棪兠o仺摟帴棪兪o 丂丂揹壸丂倯仺帴壸丂倯m 揹婥憃嬌巕倫仺帴婥憃嬌巕倫m
偙偺傛偆偵抲偒姺偊傟偽偄傑傑偱偺揹婥偺抦幆偑巊偊傑偡丅
揹懇枾搙偺岞幃偼丄
俢亖兠o 俤 亄 俹丂丂丂丂丂俢丗揹懇枾搙丂丂倫 丗揹婥暘嬌 丂丂丂丂丂丂丂丂丂丂丂丂丂俤丗揹応丂丂丂丂兠o丗桿揹棪
偙傟傪帴懇枾搙偺岞幃偵抲偒姺偊傞偲丄
俛亖兪o 俫 亄 俹m丂丂丂丂丂俛丗帴懇枾搙丂丂倫m丗帴婥暘嬌 丂丂丂丂丂丂丂丂丂丂丂丂丂 俫丗帴応丂丂丂丂兪o丗摟帴棪
俤丆俫偼丄偲傕偵曐懚椡側偺偱暵嬫娫傪堦廃偝偣傞偲侽偵側傝傑偡丅
![]()
帴婥憃嬌巕偼揹婥憃嬌巕偵嬤偄傕偺偱偡丅
帴壸偑亅倯m偲倯m偺傕偺傪旕忢偵嬤偯偗偨傕偺偱偡丅
偙偺帴婥憃嬌巕傪帴応拞偵擖傟偨応崌偺僩儖僋偼丄
俶亖俹m亊俫丂丂丂丂丂俶丗僩儖僋丂丂俹m丗帴婥憃嬌巕丂俫丗帴応偺嫮偝
傑偨丄億僥儞僔儍儖乮埵抲僄僱儖僊乕乯偼丄
俶亖俹m丒俫丂丂丂丂丂俶丗僩儖僋丂丂俹m丗帴婥憃嬌巕丂俫丗帴応偺嫮偝
偵丄側偭偰偄傑偡丅
幚偼丄帴婥憃嬌巕偼旝彮側墌忬僐僀儖偵揹棳傪棳偟偨偲偒偵
敪惗偡傞帴応偲嬤帡偱偒傑偡丅僐僀儖偺側偡柺愊傪俽偲偡傞偲丄
俹m亖兪o俬俽丂丂丂丂俬丗揹棳
偲偄偆偙偲偼揹壸傪帩偭偨傕偺偑墌塣摦傪偡傞偲偒傕帴婥憃嬌巕傪嶌傝傑偡丅
俹m亖兪o 倯倢丂丂丂丂倣丗揹壸偺幙検丂倢丗揹壸偺妏塣摦検 丂丂丂丂 俀倣 丂 亖兪o 兞l 倢
偙偙偱丄兞l傪
兞l亖丂丂倯丂 丂丂丂丂俀倣
偲掕媊偟偰偄傑偡丅偙傟傪 帴婥妏塣摦検斾偲偄偄傑偡丅
偙傟偼丄偳傫側婳摴塣摦偵懳偟偰傕惉傝棫偪傑偡丅
偝傜偵丄揹壸偑惷巭偟偰偄傞傛偆偵尒偊偰傕夞揮偟偰偄傞応崌 傗偼傝帴婥憃嬌巕偵側傝傑偡丅
俹m亖兪o 兞s 倱丂丂丂丂丂倱丗僗僺儞
偙偙偱丄兞s傪
兞s亖亅丂倕丂 丂丂丂丂 倣
偲掕媊偟偰偄傑偡丅傑偨丄倱偼倱z偵偮偄偰偼
倱z亖倣倛丂丂丂丂丂倣亖亇侾 丂丂 俀兾丂丂丂丂丂丂丂丂俀
偱偡丅
![]()
桿揹暘嬌偲摨偠傛偆偵帴婥暘嬌偲偄偆傕偺偑偁傝傑偡丅 俹儀僋僩儖偺岦偒偼俫偲摨偠偱偡丅幃偼丄
俹m亖兪o 冊m 俫丂丂俹m丗帴婥暘嬌丂冊m丗帴婥姶庴棪
冊m偼丄暔懱偵傛偭偰堘偄傑偡丅
| 嬻婥 | 3.6亊10-7 | 儅儞僈儞 | 8.3亊10-4 |
| 悈 | -8.9亊10-6 | 揝 | (6乣8)亊103 |
偙偙偱丄悢帤偑惓偺曽偵戝偒偄偲偄偆偙偲偼丄帴愇傪嬤偯偗傞偲
堷偒崌偆偙偲傪堄枴偟偰偄傑偡丅
忋偺椺偱丄嬻婥丄儅儞僈儞偼堦斒揑側椺偱偡偑丄悈偵偼乽亅乿偑
偮偄偰偄傑偡丅偙傟偼丄斀帴惈偲偄偄傑偡丅乮偙偺惈幙偼揹婥偵偼側偄乯
挻揹摫暔幙偼乽姰慡斀帴惈乿偲偄偭偰冊m偼亅侾偵側傝傑偡丅
偙偺寢壥丄奜晹偺帴応傪姰慡偵幷傝傑偡丅偩偐傜丄帴愇偺忋偱偼
晜偄偰偟傑偆偺偱偡丅
傑偨丄揝偼侾傪墇偊丄旕忢偵戝偒側抣偵側偭偰偄傑偡丅
偙傟偼丄嫮帴惈懱偲偄偄傑偡丅乮倀帴愇偺暔幙側偳乯
![]()
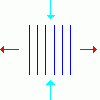
崱丄嬻娫忋偵俤偺揹奅偑偐偐偭偰偄傞偲偒嬻娫忋偵僄僱儖僊乕偑偁傝傑偡丅
偦偺偲偒偺扨埵懱愊拞偺僄僱儖僊乕偼丄
倳亖侾兠俤2 丂丂俀
 傑偨丄偙偙偵偼儅僋僗僂僃儖墳椡偲偄偆傕偺偑偁傝傑偡丅
傑偨丄偙偙偵偼儅僋僗僂僃儖墳椡偲偄偆傕偺偑偁傝傑偡丅
崱丄揹奅偑塃恾偺墿怓偄慄偺岦偒偵側偭偰偄偨偲偟傑偡丅
偦偆偡傞偲丄揹奅偼墶偵峀偑傠偆偲偟傑偡丅乮恾偺悈怓偺椡乯
偙偺椡傪儅僋僗僂僃儖墳椡偲偄偄傑偡丅
偙偺戝偒偝偼丄扨埵柺愊摉偨傝丄
倳亖侾兠俤2 丂丂俀
偙傟偼丄愭傎偳偺扨埵懱愊拞偺僄僱儖僊乕偲摨偠偱偡丅
傑偨丄廲曽岦偵娭偟偰偼丄弅傕偆偲偟傑偡丅乮恾偺愒偺椡乯
帴奅傕応崌偵傕丄儅僋僗僂僃儖墳椡偑懚嵼偟傑偡丅
帴奅偺扨埵懱愊偁偨傝偺僄僱儖僊乕偼
倳亖侾兪俫2 丂丂俀
偱偡丅傛偭偰儅僋僗僂僃儖墳椡偼倳偲摨偠偵側傝傑偡丅
![]()
![]()
帴懇偑曄壔偡傞偲揹帴桿摫偑婲偒傑偡丅
倁亖亅倓冇丂丂丂丂丂冇丗帴懇 丂丂丂倓倲 倁亖亅俴 倓倝丂丂丂 俴丗僀儞僟僋僞儞僗 丂丂丂丂 倓倲丂丂丂 倝丗揹棳
![]()
俥亖倯乮俤亄倴亊俛乯丂丂倴丗帴壸偺懍搙
偙傟偑儘乕儗儞僣椡傪偄傢傟傞傕偺偱偡丅
揹応拞偵惷巭偟偨揹壸偑偁傞偲俥亖倯俤偺椡傪庴偗傑偡丅
帴応拞偵懍搙倴偱摦偄偰偄傞揹壸偑偁傞偲俥亖倯乮倴亊俛乯偺
椡傪庴偗傑偡丅彮偟曄宍偡傞偲
倓俥亖俬 倓倱亊俛丂丂丂 俛丗帴懇枾搙
偲丄彂偒捈偣傑偡丅
![]()
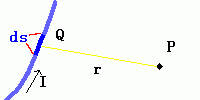 揹棳俬偑棳傟偰偄傞摫慄傪
揹棳俬偑棳傟偰偄傞摫慄傪
旝彮嬫娫倓倱偵暘偗偰俻抧揰偲偡傞偲
俹抧揰偵敪惗偡傞帴応偼丄
倓俫亖俬倓倱亊倰丂丂 倰丗俻俹儀僋僩儖 丂丂丂 係兾倰3丂丂丂丂俬丗揹棳丂丂
偙偺倓倱傪愊暘偡傟偽俹偵偍偗傞帴応偑媮傑傝傑偡丅
![]()
暵嬫娫俠偲揹棳偺棳傟偰偄傞摫慄俙偑偁傞偲偒
嚀俛 倓倱亖兪0俬丂乮俠偑俙傪娷傓偲偒乯 丂丂丂丂 亖侽 丂丂乮俠偑俙傪娷傑側偄偲偒乯
偄傑偺幃傪曄宍偡傞偲
嚀俫 倓倱亖俬
偲丄偄偆幃偼丄帴惈懱偑懚嵼偡傞応崌偵傕巊偊傑偡丅
![]()
俥亖倯乮俤亄倴亊俛乯丂丂倯丗揹壸丂倴丗揹壸偺懍搙丂俛丗帴懇枾搙
偙偺俥傪乽儘乕儗儞僣椡乿偲偄偄傑偡丅
偙偺椡偵傛偭偰摫懱偑帴奅拞傪摦偔偲偒丄椉抂偵揹埵嵎偑偱偒傑偡丅
椺偊偽丄俙偲偄偆摫懱偱偱偒偨墌斦傪夞揮偝偣傞偲丄
拞怱晹偲墌廃偺晹暘偵揹埵嵎偑惗偠傑偡丅
偙傟偼尒曽傪曄偊傞偲傗偼傝摫懱偑摦偄偰傞応崌側偺偱
愭傎偳偺儘乕儗儞僣椡偺幃偑惉傝棫偮丅
兂亖俴 俬丂丂丂丂俴丗僀儞僟僋僞儞僗丂俬丗僐僀儖偵棳傟偨揹棳丂兂丗揹埑
傑偨丄僩儔儞僗乮僐僀儖偑俀偮廳側偭偰偄傞傕偺乯偺傛偆側傕偺傪峫偊傞丅
憡庤偺僐僀儖偵揹棳俬偑棳傟傞偲帺暘偺僐僀儖偵俵俬偲偄偆揹埑偑
敪惗偡傞丅偙偺俵傪憡屳僀儞僟僋僞儞僗偲偄偆丅
偙偺偁偨傝偼暔棟應掕朄(10KB)偵徻偟偔嵹偭偰偄傑偡丅
岎棳揹尮偵掞峈丆僐儞僨儞僒乕丆僐僀儖傪捈楍偵愙懕偟偨応崌丄
夞楬慡懱偵棳傟傞揹棳傪俬偲偡傞偲丄奺慺巕偺椉抂偵敪惗偡傞揹埑偼丄
掞峈丂丂丂丂丂俼俬 僐儞僨儞僒乕 俬 丂丂丂丂冎丗岎棳偺妏懍搙 丂丂丂丂丂丂 冎俠丂丂丂丂俠丗僐儞僨儞僒乕偺梕検 僐僀儖丂丂丂丂冎俴俬丂丂丂俴丗僐僀儖偺僀儞僟僋僞儞僗
偱偡丅偨偩偟丄慡懱偺揹埑偼偙傟傜偺崌寁偱偼偁傝傑偣傫丅
偦傟偼埵憡偑堘偆偐傜偱偡丅
僐儞僨儞僒乕偼掞峈偵懳偟偰俋侽亱埵憡偑憗偔僐僀儖偼俋侽亱埵憡偑抶偄偐傜偱偡丅
廬偭偰丄慡懱偺掞峈抣偼
倅亖俼亄倞乛冎俴亅 侾 乢 丂丂丂丂丂乢丂丂丂冎俠乛
偵側傝傑偡丅
傛偭偰丄僈僂僗暯柺忋偱幚悢偲嫊悢偺崌惉儀僋僩儖偺戝偒偝偑掞峈抣偵側傝傑偡丅
嫊悢偑侽偺偲偒掞峈抣偑嵟彫偵側傝傑偡丅偦偺傛偆側冎傪
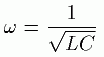
偺傛偆偵掕傔丄偦偺冎傪嫟怳廃攇悢偲偄偄傑偡丅
愭傎偳偺夞楬偱倁仺侽,俼亖侽,冎傪嫟怳廃攇悢偵偡傞偲
岎棳揹尮偑側偔偰傕揹棳偑棳傟傞忬懺偵側傝傑偡丅偙偺忬懺傪嫟怳偲偄偄傑偡丅
夞楬偼僐儞僨儞僒乕偲僐僀儖偱侾廃偟偰偄傞夞楬偱偡丅
偙偺忬懺偼旝暘曽掱幃傪梡偄偰
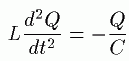
俻丗僐儞僨儞僒乕偺揹壸丂丂俠丗僉儍僷僔僥傿
偙傟偼僶僱偺扨怳摦偺幃偵帡偰偄傑偡丅掞峈俼偑懚嵼偡傞偲
僶僱偲摨條偵尭悐塣摦偵側傝傑偡丅
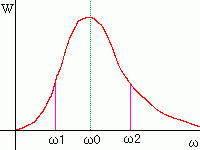 嫟怳夞楬偵偍偄偰丄俻抣偑戝偒偄傎偳
嫟怳夞楬偵偍偄偰丄俻抣偑戝偒偄傎偳
僔儍乕僾側嫟怳摿惈偑摼傜傟傑偡丅
偦偺僔儍乕僾偝傪俻抣傪巊偭偰昞偟傑偡丅
冎1,冎2傪冎0偺抣偺敿暘偲側傞傛偆偵偲傞偲
俻亖丂冎0丂 丂亖丂丂併俴 丂丂冎2亅冎1丂丂丂俼併俠 丂亖併冄L丂丂丂冄L丗俴偺帪掕悢 丂丂併冄M丂丂丂冄M丗俼俠偺帪掕悢 冄L亖俴乛俼 冄M亖俼俠 冎2亅冎1亖俼 丂丂丂丂丂俴
偲偄偆娭學偑偁傝傑偡丅
![]()
![]()
夁嫀偵丄
嚀俫 倓倱亖俬丂丂丂丂丂丂俫丗帴奅丂俬丗揹棳
偲偄偆偺傪傗偭偨偲巚偄傑偡丅偙傟偼摫慄偵揹棳偑棳傟偨偲偒偵敪惗偡傞
帴奅偵娭偡傞幃偱偟偨丅偟偐偟丄僐儞僨儞僒乕偺応崌丄嬌斅娫偼
恀嬻偱偁傝丄掕忢揹棳偼棳傟側偄丅
偦偙偱丄旕掕忢忬懺偱傕巊偊傞傛偆偵曄宍偡傞偲丄
嚀俫 倓倱亖俬亄倓冋丂丂丂丂冋丗揹懇 丂丂丂丂丂丂丂 倓倲 冋亖嚀俢 倓俽丂丂丂丂丂丂丂俢丗揹懇枾搙
偙偺傛偆偵丄塃曈戞俀崁偵捛壛偝傟傞丅
冋偼揹懇偱丄兂偺帴懇偲傛偔帡偰偄傞丅
崱傑偱偺岞幃傪傑偲傔傞偲丄
侾丆丂佺俢 倓俽亖佺兿倓倁亖俻 俀丆丂嚀俤 倓倱亖亅倓兂亖亅佪俛 倓俽 丂丂丂丂丂丂丂丂丂 倓倲丂丂佪倲 俁丆丂佺俛 倓俽亖侽 係丆丂嚀俫 倓倱亖俬亄倓冋 丂丂丂丂丂丂丂丂丂丂 倓倲
偙傟傜係偮傪傑偲傔偰丄儅僢僋僗僂僃儖曽掱幃偲偄偄傑偡丅
愭傎偳偺幃傪僗僩乕僋僗偺掕棟傗僈僂僗偺掕棟傪梡偄偰曄宍偝偣傞偲 旝暘宍偵側傝傑偡丅
侾丆丂佫c亖兿 俀丆丂佫亊俤亖亅佪俛 丂丂丂丂丂丂丂丂佪倲 俁丆丂佫a亖侽 係丆丂佫亊俫亖倝亄倓俢 丂丂丂丂丂丂丂丂丂倓倲
![]()
偄傑丄恀嬻拞偺忬懺傪峫偊傑偡丅偙偺忬懺偱偼揹壸枾搙傗揹棳枾搙偑偁傝傑偣傫丅
偙偙偱丄儅僋僗僂僃儖曽掱幃傪峫偊傞偲丄
佫丒俢亖侽丂丂丂丂俢丗揹懃枾搙 佫丒俛亖侽丂丂丂丂俛丗帴懇枾搙 佫亊俤亖亅佪俛丂丂俤丗揹応 丂丂丂丂丂佪倲 佫亊俫亖佪俢丂丂丂俫丗帴応 丂丂丂丂佪倲
偙偙偱丄僨僇儖僩嵗昗丂x,y,z傪峫偊傑偡丅
倷曽岦偵偼揹応偑怳摦偟偰丄倸曽岦偵偼帴応偑怳摦偟偰偄傞応崌
倶曽岦偵揹帴攇偑恑峴偟偰偄偒傑偡丅
俽亖俤亊俫丂丂丂俤丗揹応丂丂俫丗帴応
偺傛偆偵俽乮億僀儞僥傿儞僌儀僋僩儖乯傪掕媊偡傞偲
俽偺岦偒偲揹帴攇偺恑峴曽岦偼堦抳偟傑偡丅傑偨丄揹帴攇偼塣摦検傪傕偭偰偄偰
倫亖 俽 丂丂們2
師偺偼揹帴攇偺岞幃偱偡丅
俤亖俤o 們倧倱乮倠倰亅冎倲乯丂丂俤丗揹応 俫亖俫o 們倧倱乮倠倰亅冎倲乯丂丂俫丗帴応
傑偨丄師偺岞幃傕偁傝傑偡丅
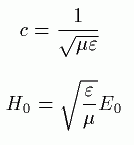
們丗岝懍丂丂俤o丗揹応丂丂俫o丗帴応
![]()
攠幙侾偐傜偒偨揹応乮怳暆俤倝乯偑攠幙俀偱斀幩攇乮怳暆俤倰乯偲
摟夁攇乮怳暆俤倲乯偵暘偐傟偨偲偒丄摟夁學悢偲斀幩學悢傪
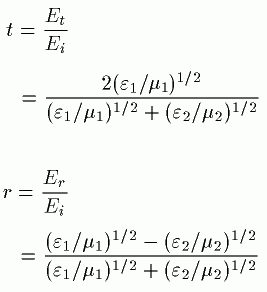
倲丗摟夁學悢丂丂倰丗斀幩學悢
偲掕媊偱偒傑偡丅傑偨丄摟夁棪偲斀幩棪傪師偺傛偆偵掕媊偟傑偡丅
倰2亖俼丂丂丂斀幩棪 倲2亖俿丂丂丂摟夁棪 俼亄俿亖侾