![]()
![]()
| 侾丆忢旛暘曽掱幃 | 俤倳倢倕倰朄丂俼倳値倗倕亅俲倳倲倲倎朄丂儗億乕僩 |
| 俀丆曃旝暘曽掱幃 (13KB) | 俤倳倢倕倰朄丂Crank-Nicholson朄丂儗億乕僩 |
| 俁丆妋棪榑 (13KB) | 儌儞僥僇儖儘朄丂儗億乕僩 |
暔棟偺朄懃偼丄旝暘曽掱幃偺宍偱昞偝傟傞偙偲偑懡偄偱偡丅偨偲偊偽丄
俥亖倣 倓2倶 丂丂丂 倓倲2
偲偄偆偺偼丄俀奒旝暘曽掱幃偵側偭偰偄傑偡丅
旝暘曽掱幃偺庬椶偼暔棟悢妛俀(17KB)偱傕愢柧偟偨偺偱偡偑
忢旝暘曽掱幃偲曃旝暘曽掱幃偺俀庬椶偑偁傝傑偡丅
曃旝暘曽掱幃偼乽佪乿偲偄偆婰崋傪偮偐偄丄夝偔偺偑暋嶨偵側傝傑偡丅
(椺偲偟偰Sch.eg.傗攇摦曽掱幃)
堦斒偵丄忢旝暘曽掱幃偼師偺傛偆偵側傝傑偡丅
倓倶(t) 亖丂倖(倶丆倲) 倓倲
偙傟偼丄倶偺師尦偑侾偺帪側偺偱丄値師尦偺忢旝暘曽掱幃偼
崱偺幃偑値屄偮偔傞昁梫偑偁傝傑偡丅
![]()
偙偙偱偼娙扨偺偨傔丄侾師尦偺旝暘曽掱幃偵偮偄偰峫偊傑偡丅
倓倶(t) 亖丂倖(倶丆倲) 倓倲
偲偄偆娭學偐傜
倶(倲亄嚈倲)丂亖丂倶(倲)丂亄丂(嚈倲)倖(倶丆倲)
偙傟偼丄倶傪俿倎倢倧倰揥奐偟偰丄侾師偺崁傑偱庢傝擖傟偨傕偺偱偡丅
偨偩丄侾師偺崁傑偱偟偐庢傝擖傟偰偄側偄偺偱岆嵎偼戝偒偔側傝傑偡丅
栤戣 倶亄冎倶亖侽 偱昞偝傟傞塣摦偺丄埵憡嬻娫偱偺摦偒傪昞偟側偝偄丅 偨偩偟丄幙検偼倣亖侾 倫亖倓倶丂偲偡傞丅 丂丂倓倲 夝摎 崱夞偼丄倶偲倫偺俀師尦偺忢旝暘曽掱幃傪夝偔偙偲偵側傝傑偡丅 倓倶亖倫丂丂丂丂倓倫亖亅冎2倶 倓倲丂丂丂丂丂丂倓倲 埲忋偺娭學偐傜Euler朄偱偼師偺傛偆偵側傝傑偡丅 倶(倲亄嚈倲) 亖 倶(倲) 亄 丂倫(倲)嚈倲 倫(倲亄嚈倲) 亖 倫(倲) 亅冎2倶(倲)嚈倲 僾儘僌儔儉偼埲壓偺捠傝偱偡丅 (SGL傪巊偭偰偄傑偡丅怓偺愰尵側偳偼徣棯偟偰偄傞偺偱偙偺傑傑偱偼摦偒傑偣傫丅)
main()
{
char c;
float omega;
float x, p, xnew, pnew;
float delt, etot;
int itime,ntime;
x = 1.0;
p = 0.0;
ntime = 5000;
printf("Enter omega & delt \n");
scanf("%f %f",&omega, &delt);
for(itime = 1; itime <= ntime; itime++) {
xnew = x + delt*p;
pnew = p - delt*omega*omega*x;
x = xnew;
p = pnew;
sgl_color(SGL_YELLOW);
sgl_disc(x,p,0.05);
sgl_display2();
if(itime - (itime/10)*10 == 0)
{
etot = p*p/2.0 + omega*omega*x*x/2.0;
printf("itime = %d etot = %f \n",itime,etot);
}
}
printf("Hit return to terminate \n");
scanf("%c",&c);
}
偙傟傪幚峴偡傞偲丄墌偵側傜偢峀偑偭偰偄偭偰偟傑偄傑偡丅
偙傟偼丄戝偒側岆嵎偑懚嵼偡傞偨傔偱偡丅

![]()
俼倳値倗倕亅俲倳倲倲倎朄偼丄俤倳倢倕倰朄偲斾傋傞偲幃偼暋嶨側偺偱偡偑
惛搙偼侾侽侽侽攞偵側傝傑偡丅(桳岠悢抣偑俁寘傾僢僾偟偨偺偱)
幃偼師偺傛偆偵側傝傑偡丅
倶(倲亄嚈倲)亖倶(倲)亄(倎亄俀倐亄俀們亄倓)嚈倲乛俇 丂丂丂倎亖倖(倶丆倲) 丂丂丂倐亖倖(倶亄倎嚈倲乛俀丆倲亄嚈倲乛俀) 丂丂丂們亖倖(倶亄倐嚈倲乛俀丆倲亄嚈倲乛俀) 丂丂丂倓亖倖(倶亄們嚈倲丆倲亄嚈倲)
椺丂(侾曄悢偺応崌) 倖(x,t)亖俀倶丂偺応崌 倎亖俀倶 倐亖俀(倶亄倎嚈倲乛俀) 們亖俀(倶亄倐嚈倲乛俀) 倓亖俀(倶亄們嚈倲) 倶(倲亄嚈倲)丂亖丂倶(倲)丂亄丂(倎亄俀倐亄俀們亄倓)嚈倲乛俇
傑偨丄懡曄悢偺応崌偼師偺傛偆偵側傝傑偡丅
倶i(倲亄嚈倲)亖倶i(倲)亄(倎i亄俀倐i亄俀們i亄倓i)嚈倲乛俇 丂丂丂倎i亖倖i(倶1丆丒丒丆倶n丆倲) 丂丂丂倐i亖倖i(倶1亄倎1嚈倲乛俀丆丒丒丆倶n亄倎n嚈倲乛俀丆倲亄嚈倲乛俀) 丂丂丂們i亖倖i(倶1亄倐1嚈倲乛俀丆丒丒丆倶n亄倐n嚈倲乛俀丆倲亄嚈倲乛俀) 丂丂丂倓i亖倖i(倶1亄們1嚈倲丂丂丆丒丒丆倶n亄們n嚈倲丂丂丆倲亄嚈倲)
栤戣丂(懡曄悢偺応崌) 乽俤倳倢倕倰朄乿偺栤戣傪俼倳値倗倕亅俲倳倲倲倎朄偱夝偒側偝偄丅 夝摎 僾儘僌儔儉偼愭傎偳偺墿怓偺晹暘傪師偺傛偆偵彂偒姺偊傑偡丅 偙偙偱拲堄偡傞偲偙傠偼丄a1,a2,b1,丒丒丒d1,d2偺弴偵彂偔偙偲偱偡丅
main()
{
char c;
float omega;
float x, p, xnew, pnew;
float delt, etot;
int itime,ntime;
float a1,a2,b1,b2,c1,c2,d1,d2;
x = 1.0;
p = 0.0;
ntime = 5000;
printf("Enter omega & delt \n");
scanf("%f %f",&omega, &delt);
for(itime = 1; itime <= ntime; itime++) {
a1=p;
a2=-omega*omega*x;
b1=p+a2*delt/2.0;
b2=-omega*omega*(x+a1*delt/2.0);
c1=p+b2*delt/2.0;
c2=-omega*omega*(x+b1*delt/2.0);
d1=p+c2*delt;
d2=-omega*omega*(x+c1*delt);
xnew = x + (a1+2*b1+2*c1+d1)*delt/6.0;
pnew = p + (a2+2*b2+2*c2+d2)*delt/6.0;
x = xnew;
p = pnew;
sgl_color(SGL_YELLOW);
sgl_disc(x,p,0.05);
sgl_display2();
if(itime - (itime/10)*10 == 0)
{
etot = p*p/2.0 + omega*omega*x*x/2.0;
printf("itime = %d etot = %f \n",itime,etot);
}
}
printf("Hit return to terminate \n");
scanf("%c",&c);
}
偙傟傪幚峴偡傞偲埲壓偺嵍偺傛偆側墌偵側傝傑偡丅
偙傟偼丄愭傎偳偺Euler朄偲丂攞棪丄寁嶼夞悢丄弶婜忦審偼摨偠偱偡丅
| 俼倳値倗倕亅俲倳倲倲倎朄 | 俤倳倢倕倰朄 |
 |
 |
![]()
偙偙偱偼丄乽寁嶼暔棟妛乿偺島媊偱幚嵺偵弌戣偝傟偨儗億乕僩偺栤戣偺夝曻傪夝愢偟傑偡丅
婥徾妛幰偺儘乕儗儞僣偼戝婥傪娙扨側儌僨儖偲偟偰
倓倶亖俙(倷亅倶) 倓倲 倓倷亖亅倶倸亄俼倶亅倷 倓倲 倓倸亖倶倷亅俛倸 倓倲
偲偄偆旝暘曽掱幃傪峫偊偨丅(俙丆俛丆俼偼僷儔儊乕僞)
偙偺宯傪僔儈儏儗乕僔儑儞偣傛丅
偨偩偟丄俙亖係丂俛亖俉乛俁丂俼亖俉侽偲偄偆抣傪戙擖偡傞偲偄偄丅
仸幚嵺偺壽戣偼丄
偺係戣偱偡丅
偙偙偱偼丄寁嶼晹暘偺僾儘僌儔儉傪帵偟偰偄傑偡丅
昤夋偼SGL傪巊偭偰偄傑偡偑愝掕晹暘偼徣棯偟偰偄傑偡丅
double A=4.0,B=8.0/3.0,R=80.0;
double a1,a2,a3,b1,b2,b3,c1,c2,c3,d1,d2,d3,x,y,z,xnew,ynew,znew;
double delt=0.01;
x=1.0; y=0.0; z=0.0;
for (long i=0; i<5000; i++){
a1=A*(y-x);
a2=-x*z+R*x-y;
a3=x*y-B*z;
b1=A*(y+a2*delt/2-(x+a1*delt/2));
b2=-(x+a1*delt/2)*(z+a3*delt/2)+R*(x+a1*delt/2)-(y+a2*delt/2);
b3=(x+a1*delt/2)*(y+a2*delt/2)-B*(z+a3*delt/2);
c1=A*(y+b2*delt/2-(x+b1*delt/2));
c2=-(x+b1*delt/2)*(z+b3*delt/2)+R*(x+b1*delt/2)-(y+b2*delt/2);
c3=(x+b1*delt/2)*(y+b2*delt/2)-B*(z+b3*delt/2);
d1=A*(y+c2*delt-(x+c1*delt));
d2=-(x+c1*delt)*(z+c3*delt)+R*(x+c1*delt)-(y+c2*delt);
d3=(x+c1*delt)*(y+c2*delt)-B*(z+c3*delt);
xnew=x + (a1+2*b1+2*c1+d1)*delt/6.0;
ynew=y + (a2+2*b2+2*c2+d2)*delt/6.0;
znew=z + (a3+2*b3+2*c3+d3)*delt/6.0;
x=xnew; y=ynew; z=znew;
sgl_color(SGL_YELLOW);
sgl_disc(x,y,1);
sgl_display2();
}
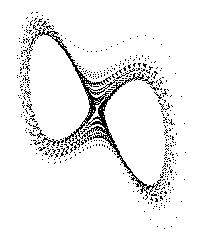
僔儈儏儗乕僔儑儞寢壥偼埲忋偺傛偆偵側傝傑偟偨丅
側偍丄僾儘僌儔儉偺僶僌傗丄弶婜抣偑晄惓側偙偲傕偁傞偺偱
偙傟偑惓夝偐偼晄妋偐偱偡丅(儈僗傪敪尒偟偨傜儊乕儖傪偔偩偝偄丅)
崱夞儗億乕僩梡偵惂嶌偟偨傾僾儕働乕僔儑儞偑偁傝傑偡丅
丒惂嶌擔丂1997/11/26(Wed) 丒Version丂0.01 丒挊嶌尃丂彫椦惉摽
偙偺俽倧倖倲偼儕儕乕僗斉側偺偱扨撈偱摦嶌偟傑偡丅