![]()
![]()
| 侾丆帴惈 | 儃乕傾帴巕丂僗僺儞帴婥儌乕儊儞僩 懷帴棪丂妀帴婥嫟柭丂嫮帴惈懱 |
| 俀丆僶儞僪棟榑 | Bloch偺掕棟丂桳岠幙検丂Brillouin堟 |
| 俁丆敿摫懱 | 摫懱丒愨墢懱丂屌桳敿摫懱丂晄弮暔敿摫懱丂揹巕暘晍丂Hall岠壥 |
| 係丆挻揱摫 | 奿巕寚娮丂挻揱摫丂挻棳摦 |
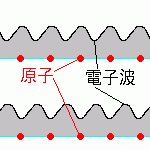
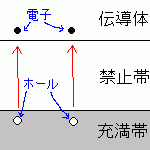
暔幙傪帴応偺拞偵擖傟傞偲帴壔偟傑偡丅
偙傟偼丄桿揹懱傪揹応偺拞偵擖傟傞偲暘嬌偡傞偺偵帡偰偄傑偡偑
帴壔偺応崌偼帴応偲斀懳岦偒偵側傞偙偲偑偁傝傑偡丅(偙傟傪斀帴惈偲偄偄傑偡丅)
傑偨丄帴応偲摨偠曽岦偵帴壔偝傟傞傕偺傪忢帴惈偲偄偄傑偡丅
揹巕偑尨巕偺廃傝傪傑傢偭偰偄傞偙偲傪峫偊傑偡丅
偙偺揹巕偺妏塣摦検偼h扨埵偵側傝傑偡丅
傑偨丄揹巕偑墌塣摦傪偟偰偄傞偺偱帴応偑敪惗偟傑偡丅
偙偺偲偒丄妏塣摦検偑検巕壔偝傟偰偄傞偨傔帴応傕検巕壔偝傟傑偡丅
偦偺婎杮揑側扨埵偼
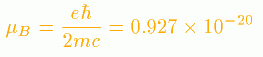
偲側傝傑偡丅偙傟偐傜幚嵺偺妏塣摦検偼
![]()
偲側傝傑偡丅倢偼帴婥偺検巕悢偱侽丆侾丆俀丒丒側偳偺惍悢偑擖傝傑偡丅
![]()
揹巕帺恎傕帺揮偵傛偭偰帴婥傪惗偠傑偡丅
廬偭偰丄幚嵺偺帴婥偼婳摴帴婥儌乕儊儞僩偲僗僺儞帴婥儌乕儊儞僩偺
儀僋僩儖揑側榓偵側傝傑偡丅幚嵺偺帴婥儌乕儊儞僩偼
兪亖亅俀兪Bh倱
偱偡丅愭傎偳偺幃偲斾傋傞偲俀偲偄偆學悢偑偐偐偭偰偄傑偡丅
偙偙偱丄幃傪堦斒壔偡傞偨傔偵倗場巕偲偄偆傕偺傪摫擖偟傑偡丅
倗場巕偼妏塣摦検偺庬椶偵傛偭偰埲壓偺傛偆偵曄壔偟傑偡丅
| 庬椶 | 倗場巕偺抣 |
| 婳摴妏塣摦検 | 侾 |
| 僗僺儞妏塣摦検 | 俀 |
| 慡妏塣摦検 | 僗僺儞偲婳摴偵傛偭偰曄傢傞 |
偦偆偡傞偙偲偱帴婥儌乕儊儞僩偼
兪亖亅倗兪Bh倞
偱偒傑傝傑偡丅(倞偼検巕悢)
![]()
奜晹偺帴応偵傛偭偰丄暔懱偺撪晹偱帴壔偑惗偠傑偡丅
偙偺妱崌偼懷帴棪冊偱昞偣傞偙偲偼丄乽揹帴婥妛俀(21KB)乿偱妛傃傑偟偨丅
冊亜侽偺帪傪乽忢帴惈懱乿丄冊亙侽偺帪傪乽斀帴惈懱乿偲偄偄傑偡丅
偨偄偰偄偺暔幙偼暵妀峔憿傪偲傞偺偱冊亖侽偵側傝傑偡丅
 屆揟揑偵懷帴棪傪夝偔偲
屆揟揑偵懷帴棪傪夝偔偲
亙兪z亜亖丂丂侾丂丂丂丂亅丂侾 丂兪B丂丂倲倎値倛(倎)丂丂丂倎
偙偺傛偆偵側傝傑偡丅
偙偺娭悢傪乽俴倎値倗倕倴倝値偺幃乿偲偄偄傑偡丅
偟偐偟幚嵺偵偼検巕揑側岠壥偑偁傝
偁傞曽岦偺惉暘偼偲傃偲傃偺抣偟偐
偲傟側偄偲偄偆摿挜偑偁傝傑偡丅
偙偺傛偆側検巕揑側岠壥傪庢傝擖傟傞偲
亙兪z亜亖倲倎値倛(倎) 丂兪B
塃恾偼丄屆揟揑側傕偺偲検巕榑揑側傕偺偺僌儔僼傪帵偟偨傕偺偱偡丅
嬥懏偺応崌偼丄冊p偱昞偡偙偲偑偱偒Pauli偺忢帴惈偲偄偄傑偡丅
傑偨丄揱摫揹巕傪帩偮偺偱丄庛偄Landau偺斀帴惈偑偁傝傑偡丅
偙傟傪Landau偺斀帴惈冊d偱昞偟傑偡丅
偝傜偵丄僀僆儞偵傛傞傕偺傪冊ion偲偡傞偲幚嵺偺懷帴棪偼
冊亖冊p亄冊d亄冊ion
偵側傝傑偡丅
![]()
晄懳揹巕傪侾屄傕偮暘巕偵帴応傪偐偗傞偲
亇兪B俫
偩偗僄僱儖僊乕偑曄壔偟傑偡丅偙偙偵奜晹偐傜
倛兯亖俀兪B俫
偩偗偺揹帴攇僄僱儖僊乕傪梌偊偰傗傞偲丄揹巕偼嫟柭偟
壓偐傜忋偺僄僱儖僊乕忬懺偵堏摦偟傑偡丅
偙傟傪乽揹巕僗僺儞嫟柭乿(俤俽俼)偲偄偄傑偡丅
栤戣 揹巕偺嫟柭偡傞廃攇悢傪媮傔傛 偨偩偟丄奜晹帴応偼俆侽侽侽僈僂僗偲偡傞 夝摎 兯亖俀兪B俫 丂丂丂 倛丂 丂亖侾係俧俫倸
傑偨丄梲巕傕帴婥僗僺儞傪帩偪傑偡丅
兪p亖侾丏係侾亊侾侽-23
偙傟偼丄揹巕偺応崌偲斾傋傞偲寘堘偄偵彫偝側抣偱偡丅
栤戣 梲巕偺嫟柭偡傞廃攇悢傪媮傔傛 偨偩偟丄奜晹帴応偼侾侽4僈僂僗偲偡傞 夝摎 兯亖俀兪p俫 丂丂丂 倛丂 丂亖係俀丏俇俵俫倸
梲巕偺応崌丄妀帴婥嫟柭(俶俵俼)偲偄偄傑偡丅
![]()
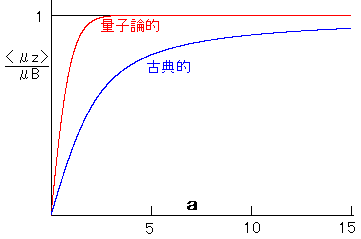
 忢帴惈懱偼帴応俫傪偐偗傞偲丄偦傟偵斾椺偟偰
忢帴惈懱偼帴応俫傪偐偗傞偲丄偦傟偵斾椺偟偰
帴壸俵傪帩偪傑偡丅(塃恾偺巼怓偺捈慄)
偦傟偵懳偟偰嫮帴惈懱偼愒亄椢怓偺嬋慄偺傛偆側曄壔傪偟傑偡丅
嵟弶丄嫮帴惈懱偵偼帴応偑偐偐偭偰偄傑偣傫丅
偦偙偵帴応傪偐偗傞偲媫寖偵帴壸傪帩偪傑偡丅
傗偑偰帴壸偑朞榓偟傑偡丅
偙偙偱丄帴応傪庢傝嫀偭偰傕帴壸偑巆偭偨忬懺偵側傝傑偡丅 (帺敪帴壔)
偙傟偑嫮帴惈懱偺摿挜偱丄俫俢丆俥俢偺帴婥柺傗 Video僥乕僾偵巊傢傟傑偡丅
偙偺嫮帴惈懱偼壏搙傪忋徃偝偣偰丄僉儏儕乕揰俿們埲忋偵偡傞偲 偨偩偺忢帴惈懱偵側偭偰偟傑偄傑偡丅 帴愇傪擬偡傞偲帴壸偑側偔側偭偰偟傑偆偺偼偙偺偨傔偱偡丅
帴壸偑側偔側傞棟桼偲偟偰丄掅壏偱偼帴婥僗僺儞偑摨偠曽岦傪岦偄偰 僄僱儖僊乕傪摼偟傛偆偲偟傑偡丅偙偺偲偒偼嫮帴惈懱偵側傝傑偡丅 偟偐偟丄崅壏偱偼帴婥僗僺儞摨巑偼摨偠曽岦傪岦偄偰僄僱儖僊乕傪 摼偡傞昁梫偑側偔側傝傑偡丅偙偺偲偒偼忢帴惈懱偵側傞傢偗偱偡丅
寢徎撪偺尨巕偼摍娫妘偵暲傫偱偄傑偡丅 偙偺偲偒偺尨巕娫嫍棧傪倎偲偡傞偲
兊k(x)亖eikxuk(x)
偺傛偆偵側傝傑偡丅(u偼億僥儞僔儍儖)
uk(x)亖uk(x+a)
偲偄偆廃婜娭悢偵側傝傑偡丅 偙偺偙偲傪Bloch偺掕棟偲偄偄傑偡丅
![]()
寢徎拞偱偼揹巕偼攇摦惈傪帵偟傑偡丅
偦偺偨傔丄孅愜棪値偺寢徎拞偱偼兩偑曄壔偟傑偡丅
偙偺塭嬁偵傛偭偰揹巕偺幙検偑廳偔側偭偨傛偆側怳傞晳偄傪帵偟傑偡丅
偙偺乽廳偄乿揹巕偺幙検傪丂倣*偱昞偟偰乽桳岠幙検乿偲偄偄傑偡丅
 揹巕偺攇悢傪倠丄僄僱儖僊乕傪俤偲偡傞偲
揹巕偺攇悢傪倠丄僄僱儖僊乕傪俤偲偡傞偲
塃恾偺傛偆側娭學偑惉傝棫偪傑偡丅
僄僱儖僊乕偲倠偺娭學偼
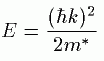
側偺偱曻暔慄忋偵側傝傑偡丅(恾拞忋偺僺儞僋)
偟偐偟丄倠亖亄亅兾乛倎偱偼攇偼掕嵼攇偵側偭偰偟傑偄
恑峴偟傑偣傫丅偙偙偱孮懍搙倴偼
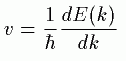
偱昞偣丄倴亖侽側偺偱僄僱儖僊乕偺孹偒偼侽偱偁傞昁梫偑偁傝傑偡丅
偙偺岠壥偵傛偭偰幚嵺偵偼恾拞偺愒慄偺傛偆偵怳傞晳偄傑偡丅
偲偙傠偱丄攇悢倠偼俀兾乛倎偺廃婜偑偁傞偺偱
塃恾壓偺傛偆偵堏摦偱偒傑偡丅(忋恾塃忋傪壓恾嵍拞墰丒丒偺傛偆偵)
 偙偺俤倗偑偱偒傞尰徾傪尨巕儌僨儖偱峫偊偰尒傑偟傚偆丅
偙偺俤倗偑偱偒傞尰徾傪尨巕儌僨儖偱峫偊偰尒傑偟傚偆丅
捠忢偼揹巕偺攇挿偲奿巕娫妘偼柍娭學偱偡丅
偟偐偟丄倠亖亄亅兾乛倎偱偼揹巕偺攇挿偲奿巕娫妘偑堦抳偡傞偨傔
塃恾偺傛偆偵2捠傝偺応崌偑峫偊傜傟傑偡丅
堦曽偼尨巕偺嬤朤偵揹巕偑懚嵼偡傞応崌(忋恾)偱偡丅
偙偺応崌偼揹巕偺僄僱儖僊乕偼掅偔偰偡傒傑偡丅
傕偆堦曽偼尨巕娫偵懚嵼偡傞応崌(壓恾)偱僄僱儖僊乕偼
崅偔側傝傑偡丅偙傟傜偺僄僱儖僊乕嵎偑俤倗偱偡丅
偙偺嬋慄摨巑偺寗娫傪僄僱儖僊乕僊儍僢僾俤倗偱昞偟
僄僱儖僊乕偑懚嵼偟摼傞応強傪僶儞僪偲偄偄傑偡丅
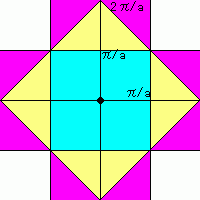
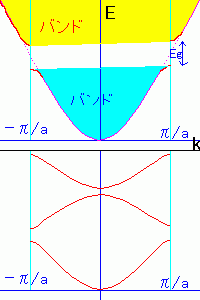
俀師尦偺Brillouin堟偼塃偺傛偆偵側傝傑偡丅
慜恾偱曻暔慄偺掙偵側偭偰偄偨晹暘偼
悈怓偵側偭偰偄傑偡丅(戞侾Brillouin堟)
師偵尨揰偵嬤偄椞堟偼戞俀Brillouin堟偲傛偽傟
墿怓丄師偑戞俁rillouin堟偱巼丒丒偲側偭偰偄傑偡丅
偄偢傟傕俀兾乛倎偛偲偵廲墶偵偢傜偡偙偲偱拞墰偺
戞侾Brillouin堟偵廤傔傜傟傑偡丅(柺愊偼曄傢傜側偄)
摫懱偼愭掱偺Brillouin椞堟偵揹巕偑枮偨偝傟偰偄傑偣傫丅
偙偺偨傔丄揹応偑偱偒傞偲揹巕偑僔僼僩偟偰丄揹巕偺暘晍偵
曃傝偑偱偒傑偡丅偙傟偑揹婥偺捠傞棟桼偱偡丅
偦傟偵懳偟偰愨墢懱偼丄偳偺僶儞僪傕揹巕偑枮偨偝傟偰偄傞偐嬻偱偡丅
揹巕偑嬻偺偲偙傠偱偼傕偪傠傫揹巕偼捠傝傑偣傫丅
揹巕偑枮偨偝傟偰偄傞偲偙傠偵揹応傪偐偗傞偲揹巕偑僔僼僩偟傑偡丅
偟偐偟丄偙偺僶儞僪偼枮偨偝傟偰偄傞偺偱揹巕偺曃傝偼偱偒傑偣傫丅
(偮傑傝丄嵍塃偺揹巕偺悢偼摨悢偱偡丅)
偙偺偨傔揹棳偼棳傟傑偣傫丅
![]()
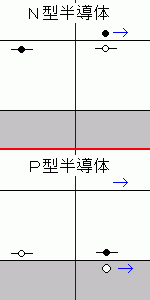
 敿摫懱偺揹婥揑惈幙偼丄愨墢懱偲摫懱偺拞娫揑惈幙傪帩偭偰偄傑偡丅
偟偐偟丄壏搙側偳偺曄壔偵傛偭偰摫懱偵側偭偨傝愨墢懱偵側偭偨傝偟傑偡丅
偙偺棟桼偼塃恾偱愢柧偱偒傑偡丅
敿摫懱偺揹婥揑惈幙偼丄愨墢懱偲摫懱偺拞娫揑惈幙傪帩偭偰偄傑偡丅
偟偐偟丄壏搙側偳偺曄壔偵傛偭偰摫懱偵側偭偨傝愨墢懱偵側偭偨傝偟傑偡丅
偙偺棟桼偼塃恾偱愢柧偱偒傑偡丅
愨墢懱偲偄偆偺偼僶僀儞僪撪偵偼揹巕偑枮偨偝傟偰偄傞偐丄嬻偺忬懺偵側偭偰偄傑偡丅
恾偱偼廩枮懷偵揹巕偑枮偨偝傟丄揱摫懷偵偼揹巕偑偁傝傑偣傫丅
摫懱偼揱摫懷偵揹巕偑懚嵼偟丄姰慡偵偼枮偨偝傟偰偄側偄偺偱揱摫惈傪帵偟傑偡丅
敿摫懱偼愨墢懱偵帡偨揹巕攝抲傪偟偰偄傑偡丅
偟偐偟嬛巭懷偺暆(僄僱儖僊乕僊儍僢僾俤倗)偑旕忢偵彫偝偔丄忢壏偱傕
揹巕偑揱摫懷偵椼婲偟丄揱摫惈傪帵偟傑偡丅
![]()
 俽倝丆俧倕側偳扨懱偺敿摫懱偼乽恀惈敿摫懱乿偲偄偄傑偡丅
偟偐偟丄偙傟偵俁壙偁傞偄偼俆壙偺晄弮暔傪彮検擖傟傞偲曄傢偭偨惈幙傪帵偟傑偡丅
俽倝傗俧倕偼係壙偺尨巕側偺偱偦偙偵俆壙偺尨巕(俹尦慺側偳)傪擖傟傞偲揹巕偑係偮偩偗
寢崌偱偒側偄忬懺偵側傝傑偡丅偙偺揹巕偼尨巕偵揹婥揑側庛偄懇敍傪庴偗傑偡丅
偙偺傛偆側揹巕偼娙扨偵揱摫懷偵椼婲偟偰揹婥揱摫惈傪帵偟傑偡丅
偙傟傪愭掱偺恾偱愢柧偡傞偲丄弶婜偺忬懺偱偼嵍忋偺傛偆偵偐側傝揱摫懷偵嬤偄偲偙傠偵偁傝傑偡丅
偦偙偵偪傚偭偲偟偨僄僱儖僊乕偼壛傢傞偲塃忋偺傛偆偵揹巕偑揱摫懷偵椼婲偟偰
儂乕儖偑巆傝傑偡丅偙偺傛偆側揹巕傪曻弌偡傞敿摫懱傪俶宆敿摫懱偲偄偄傑偡丅
斀懳偵俁壙偺尨巕傪晄弮暔偲偟偰擖傟偨応崌丄嵍壓偺傛偆偵側偭偰偄偰
僄僱儖僊乕偑梌偊傜傟傞偲廩枮懱偐傜揹巕偑椼婲偟偰丄廩枮懱偵儂乕儖偑偱偒傑偡丅
偙偺傛偆側揹巕傪媧廂偡傞敿摫懱傪俹宆敿摫懱偲偄偄傑偡丅
俽倝丆俧倕側偳扨懱偺敿摫懱偼乽恀惈敿摫懱乿偲偄偄傑偡丅
偟偐偟丄偙傟偵俁壙偁傞偄偼俆壙偺晄弮暔傪彮検擖傟傞偲曄傢偭偨惈幙傪帵偟傑偡丅
俽倝傗俧倕偼係壙偺尨巕側偺偱偦偙偵俆壙偺尨巕(俹尦慺側偳)傪擖傟傞偲揹巕偑係偮偩偗
寢崌偱偒側偄忬懺偵側傝傑偡丅偙偺揹巕偼尨巕偵揹婥揑側庛偄懇敍傪庴偗傑偡丅
偙偺傛偆側揹巕偼娙扨偵揱摫懷偵椼婲偟偰揹婥揱摫惈傪帵偟傑偡丅
偙傟傪愭掱偺恾偱愢柧偡傞偲丄弶婜偺忬懺偱偼嵍忋偺傛偆偵偐側傝揱摫懷偵嬤偄偲偙傠偵偁傝傑偡丅
偦偙偵偪傚偭偲偟偨僄僱儖僊乕偼壛傢傞偲塃忋偺傛偆偵揹巕偑揱摫懷偵椼婲偟偰
儂乕儖偑巆傝傑偡丅偙偺傛偆側揹巕傪曻弌偡傞敿摫懱傪俶宆敿摫懱偲偄偄傑偡丅
斀懳偵俁壙偺尨巕傪晄弮暔偲偟偰擖傟偨応崌丄嵍壓偺傛偆偵側偭偰偄偰
僄僱儖僊乕偑梌偊傜傟傞偲廩枮懱偐傜揹巕偑椼婲偟偰丄廩枮懱偵儂乕儖偑偱偒傑偡丅
偙偺傛偆側揹巕傪媧廂偡傞敿摫懱傪俹宆敿摫懱偲偄偄傑偡丅
![]()
揹巕偼埲壓偺Fermi暘晍偵廬偄傑偡丅
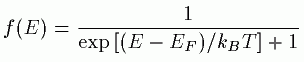
恀惈敿摫懱偱偼丄俤F偼嬛巭懷偺傎傏拞墰偵偁傝傑偡丅
偟偐偟丄嬛巭懷偵偼揹巕偼懚嵼偟側偄偺偱丄偙偺晹暘偼峫偊傑偣傫丅
峫嶡偡傞偺偼丄揱摫懷偵傢偢偐偵偁傞暘晍(揹巕偺暘晍)偲丄
廩枮懷偵偁傞傎偲傫偳侾偵嬤偄暘晍(儂乕儖偺暘晍)偱偡丅
値宆敿摫懱偱偼丄俤F偼嬛巭懷偺忋懁丄揱摫懷偵嬤偄偁偨傝偵偁傝傑偡丅
偦偙偱偼丄揹巕偑懡偔懚嵼偟丄儂乕儖偼傎偲傫偳偁傝傑偣傫丅
倫宆敿摫懱偱偼丄俤F偼嬛巭懷偺壓懁丄廩枮偵嬤偄偁偨傝偵偁傝傑偡丅
偦偙偱偼丄儂乕儖偑懡偔懚嵼偟丄揹巕偼傎偲傫偳偁傝傑偣傫丅
![]()
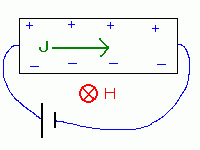
敿摫懱偵塃恾偺傛偆側帴応偑偐偐偭偰偄傞傕偺偲偟傑偡丅
偙偙偵揹棳傪棳偡偲丄儘乕儗儞僣椡偨傔偵揹応偑惗偠傑偡丅
偙傟偑乽Hall岠壥乿偱偡丅
偙偺Hall岠壥傪棙梡偡傞偙偲偵傛偭偰丄帴応偺嫮偝傪
應掕偡傞偙偲偑偱偒傑偡丅
寢徎拞撪晹偺尨巕攝楍傪峫偊偰傒傑偡丅
捠忢偼丄堦條偵尨巕偑攝楍偟偰偄傞偙偲偑憐憸偱偒傑偡丅
偟偐偟丄奿巕寚娮傕懚嵼偟傑偡丅
奿巕寚娮偼戝奣偼偮偓偺俀偮偵暘偗傞偙偲偑偱偒傑偡丅 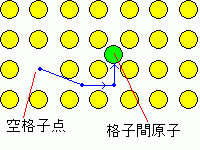
偁傞尨巕偑撍慠偲側傝偺尨巕娫偵擖傝崬傫偱
堏摦偟偰偄偔丒丒偲偄偆偺偑Frenkel寚娮偱偡丅
偙偺偲偒丄偁偄偨奿巕揰傪乽嬻奿巕揰乿
旘傫偱偄偭偨尨巕傪乽奿巕娫尨巕乿偲偄偄傑偡丅
傎偲傫偳偺応崌丄椬偵堏摦偟偰傕偡偖尦偺埵抲偵栠傝傑偡丅 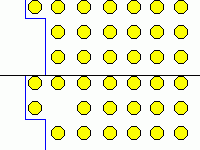
塃恾偺惵偄晹暘偑寢徎柺偲偟傑偡丅 偙偙偵尨巕偑旘傃忋偑傞偲寢徎撪偵寚娮偑偱偒傑偡丅 偙偺傛偆偵偟偰偱偒傞寚娮傪 Schottky寚娮偲偄偄傑偡丅
![]()
挻揱摫忬懺偵側傞偲師偺摿挜揑側尰徾偑婲偒傑偡丅
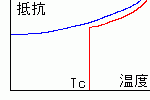 壏搙傪壓偘偰偄偒丄椪奅壏搙俿C傪壓夞傞偲
壏搙傪壓偘偰偄偒丄椪奅壏搙俿C傪壓夞傞偲
揹婥掞峈偑傎偲傫偳侽偵側傝傑偡丅
偙偺乽傎偲傫偳乿偲偄偆偺偼
姰慡偵侽偵側傞偙偲偑徹柧偝傟偨偺偱偼側偔
應掕偱偒傞斖埻撪偱侽偱偁傞偙偲傪帵偟偰偄傑偡丅
揹婥掞峈偑傎偲傫偳侽側偺偱揹棳傪堦夞棳偡偲塱媣
(偍偦傜偔侾侽偺侾侽100忔擭埲忋)偵棳傟懕偗傑偡丅
椪奅壏搙偼挻揱摫(12KB)偱愢柧偟偨暔幙偱偼俋侽[K]
嵟嬤偺崅壏挻揱摫暔幙偱偼丄150[K]掱搙偱偡丅
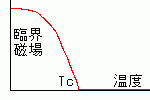 挻揱摫忬懺偵側傞偨傔偵偼丄壏搙傪椪奅壏搙埲壓偵壓偘傞偙偲傕昁梫偱偡偑
挻揱摫忬懺偵側傞偨傔偵偼丄壏搙傪椪奅壏搙埲壓偵壓偘傞偙偲傕昁梫偱偡偑
懠偵傕丄帴応傪椪奅帴応埲壓偵偡傞昁梫偑偁傝傑偡丅
椪奅帴応偼丄壏搙偺忋徃偲偲傕偵彫偝偔側偭偰偟傑偄丄
俿們偱偼侽偵側偭偰偟傑偄傑偡丅
俿亖侽偱偺椪奅帴応傕偝傎偳戝偒側傕偺偱偼偁傝傑偣傫丅 (Ti偱100gauss丄Hg偱411gauss掱搙)
偟偐偟丄偁傞庬偺崌嬥偼侾侽5gauss埲忋偱傕
懴偊傜傟傑偡丅偙偺傛偆側挻揱摫暔幙傪乽峝挻揱摫懱乿偲偄偄傑偡丅
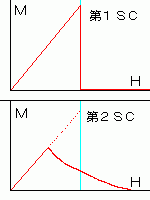 捠忢偺挻揱摫懱(埲崀丄戞侾庬挻揱摫懱)偵帴応傪偐偗傞偲
捠忢偺挻揱摫懱(埲崀丄戞侾庬挻揱摫懱)偵帴応傪偐偗傞偲
椪奅帴応傪墇偊偨帪揰偱昞柺偱帴椡慄偺埑椡偵
懴偊傜傟側偔側偭偰堦婥偵曵夡偟傑偡丅
偟偐偟丄峝挻揱摫懱(埲崀丄戞俀庬挻揱摫懱)偵
帴応傪偐偗傞偲椪奅帴応慜偵撪晹偵
偠傢偠傢偲帴椡慄偑怤擖偟傑偡丅
偦偟偰丄椪奅帴応傪墇偊偰偁傞帴応偵
払偟偨偲偒偵姰慡偵攋傟傑偡丅
乽挻揹摫帴愇乿偲屇偽傟傞偺偼戞俀庬挻揱摫懱偺偙偲偱偡丅
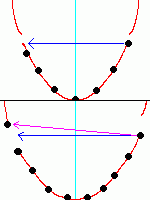 捠忢偺忢揱摫懱偱偺揹棳偺棳傟偼塃恾忋偺傛偆偵側傝傑偡丅
捠忢偺忢揱摫懱偱偺揹棳偺棳傟偼塃恾忋偺傛偆偵側傝傑偡丅
揹応偑偐偐傞偲揹巕偑僔僼僩偟傑偡丅
偦偟偰俤倗偵払偟偨揹巕偼俀兾乛倎偩偗嶶棎偝傟傑偡丅
(恾拞偺惵偄慄)偙偺傛偆偵偟偰揹棳偼尭悐偝傟偰偄偒傑偡丅
偟偐偟丄挻揱摫懱偱偼丄塣摦検偲僄僱儖僊乕偺娭學偑嵍塃懳徧偵側傝傑偣傫丅
(塃壓恾嶲徠)傕偟丄嵍塃懳徧偩偲丄愨墢懱偵側偭偰偟傑偆偐傜偱偡丅
偙偙偵揹応偑偐偐傞偲揹巕偼愭掱偺傛偆偵嶶棎偝傟傑偡丅
偟偐偟丄嵍塃旕懳徧偱偁傞偨傔偵惵慄偺傛偆偵嶶棎偝傟傞偲
嬛巭懷偵傇偮偐偭偰偟傑偆偺偱偙偺傛偆側嶶棎偼偁傝摼傑偣傫丅
偦偙偱僺儞僋怓慄偺傛偆偵嶶棎偝傟傑偡丅
嶶棎尦偺揹巕偺悢偲嶶棎愭偺揹巕偺悢偺斾偼
擬暯峵忬懺偵傛偭偰寛傑偭偰偄傑偡丅
偦偺偨傔丄堦搙偙偺傛偆側忬懺偵側傞偲塃忋偺傛偆側忬懺偵
栠傟傑偣傫丅偙傟偑塱媣揹棳偺惓懱偱偡丅
仸挻揱摫偺徻嵶偵偮偄偰偼暔惈僛儈俆傪偛棗偔偩偝偄丅
![]()
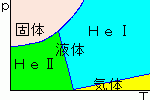 俫倕偺塼憌偵偼俀庬椶偺忬懺偑偁傝傑偡丅
俫倕偺塼憌偵偼俀庬椶偺忬懺偑偁傝傑偡丅
侾偮偼俫倕嘥偲偄偆捠忢偺塼懱僿儕僂儉偲
俫倕嘦偲偄偆挻棳摦忬懺偺僿儕僂儉偱偡丅
挻棳摦忬懺偵側傞偲丄捠忢偼昞柺挘椡偺偨傔捠傟側偄
嵶偄寠傕捠傞偙偲偑偱偒偨傝
梕婍偺懁柺傪偼偄忋偑傞偲偄偆尰徾偑婲偒傑偡丅